逻辑哲学论 (Tractatus Logico-Philosophicus)
作者:路德维希·维特根斯坦(Ludwig Wittgenstein) 维也纳,1918 年
翻译:GPT4o
路德维希·维特根斯坦(Ludwig Wittgenstein)的《逻辑哲学论》(Tractatus Logico-Philosophicus)是20世纪哲学领域最重要、也最独特的著作之一。
逻辑哲学论 的主体部分是在第一次世界大战的战场上写成的。1914年战争爆发时,本可免服兵役的维特根斯坦却选择以志愿兵身份加入了奥匈帝国军队。他希望通过面对死亡和极端的艰苦,来“拯救自己的灵魂”。 他在战壕中、在炮火声中,随身带着一个小本子,在里面记录他对逻辑、语言、伦理和上帝的思考。这些笔记最终构成了《逻辑哲学论》的草稿。战争即将结束时,维特根斯坦在意大利前线被俘,成为一名战俘。正是在意大利的战俘营里,他完成了这部著作的最终手稿。 这段经历使得《逻辑哲学论》不仅仅是一部冰冷的逻辑著作,它也包含了关于伦理、美学和“不可言说之物”(the mystical)的思考。
路德维希·维特根斯坦的《逻辑哲学论》(Tractatus Logico-Philosophicus)远非一件束之高阁的历史文物,它为理解人工智能(AI)的整个发展轨迹——从其逻辑符号主义的起源到当代神经网络面临的深刻哲学挑战——提供了一个不可或缺且经久不衰的概念框架。《逻辑哲学论》并非一份通往通用人工智能(AGI)的过时路线图,而是一份永恒且必要的指南,帮助我们理解整个事业的哲学地貌、内在局限和深远的困难。
在AI 高速发展的今天,我们用LLM翻译了路德维希·维特根斯坦 1918年发表的 《逻辑哲学论 (Tractatus Logico-Philosophicus)》,让我们重新思考下 逻辑哲学论 对AI发展的指导意义。
1. 世界是所有“是其所是”的东西(The world is all that is the case)。
1.1 世界是事实的总和,而非事物的总和。
1.11 世界由事实决定,并由所有这些事实决定。
1.12 因为事实的总和决定了是其所是的东西,以及所有“不是其所是”的东西。
1.13 逻辑空间中的事实就是世界。
1.2 世界分解为事实。
1.21 在其他一切保持不变的情况下,每一项都可以是其所是或不是其所是。
2. 是其所是的东西——一个事实——是事态(states of affairs)的存在。
2.01 一个事态(事物的一种状态)是客体(objects/things)的一种组合。
2.011 对于客体来说,它们能够成为事态的可能构成要素是本质性的。
2.012 在逻辑中,没有什么是偶然的:如果一个事物可以在一个事态中出现,那么该事态的可能性必须已铭写在事物本身之中。
2.0121 如果一个情境恰好符合一个已经可以完全独立存在的事物,这似乎是一种偶然。如果事物可以在事态中出现,这种可能性就必须从一开始就存在于它们之中。(在逻辑的领域中,没有什么可以是仅仅可能的。逻辑处理每一种可能性,所有可能性都是它的事实)。正如我们完全无法想象空间对象在空间之外或时间对象在时间之外一样,我们同样无法想象任何一个被排除在与其他事物结合的可能性之外的客体。如果我能想象客体在事态中结合,我就不能想象它们被排除在这些组合的可能性之外。
2.0122 事物是独立的,因为它们可以出现在所有可能的情境中,但这种独立形式是与事态的一种关联形式,是一种依赖形式。(词语不可能以两种不同的角色出现:单独出现,和在命题中出现)。
2.0123 如果我认识一个客体,我也就知道它在事态中的所有可能出现情况。(所有这些可能性都必须是客体本质的一部分)。新的可能性不可能在事后才被发现。
2.01231 如果我要认识一个客体,尽管我不必知道它的外部属性,但我必须知道它的所有内部属性。2.0124 如果所有客体都给定了,那么所有可能的事态也就同时给定了。
2.013 每个事物,可以说是处于一个可能的事态空间之中。我可以想象这个空间是空的,但我不能想象没有这个空间的事物。
2.0131 一个空间客体必须位于无限空间中。(一个空间点是一个论证位置)。视觉领域中的一个斑点,尽管不一定是红色的,但必须有某种颜色:它可以说是被颜色空间所包围。音符必须有某种音高,触觉客体必须有某种硬度等级,等等。
2.014 客体包含了所有情境的可能性。
2.0141 它出现在事态中的可能性是客体的形式。
2.02 客体是简单的。
2.0201 关于复合体的每一个陈述都可以分解为关于其构成要素的陈述,以及完全描述这些复合体的命题。
2.021 客体构成了世界的实体。这就是它们不能是复合体的原因。
2.0211 如果世界没有实体,那么一个命题是否有意义将取决于另一个命题是否为真。
2.0212 在那种情况下,我们将无法勾勒出世界的任何图景(无论是真是假)。
2.022 显而易见,一个想象中的世界,无论它与现实世界有多么不同,都必须与现实世界有某种共同之处——即一种形式。
2.023 客体正是构成了这种不可改变的形式。
2.0231 世界的实体只能决定一种形式,而不能决定任何物质属性。因为物质属性只是通过命题来表征的——只有通过客体的配置才能产生它们。
2.0232 从某种意义上说,客体是无色的。
2.0233 如果两个客体具有相同的逻辑形式,那么除了它们的外部属性之外,它们之间唯一的区别就是它们是不同的。
2.02331 一个事物要么拥有其他任何事物都没有的属性,在这种情况下,我们可以立即使用描述来将其与其他事物区分开并指称它;要么,另一方面,有几个事物共同拥有全部属性,在这种情况下,根本不可能指出其中之一。因为如果没有任何东西能区分一个事物,我就无法区分它,否则它毕竟会被区分开。
2.024 实体是独立于是其所是之物而存在的东西。
2.025 它是形式和内容。
2.0251 空间、时间、颜色(有颜色)是客体的形式。
2.026 如果世界要具有不可改变的形式,就必须有客体。
2.027 客体、不可改变的和持续存在的是同一回事。
2.0271 客体是不可改变和持续存在的东西;它们的配置是变化和不稳定的东西。
2.0272 客体的配置产生了事态。
2.03 在一个事态中,客体相互契合,如同链条的环节。
2.031 在一个事态中,客体彼此处于确定的关系中。
2.032 客体在一个事态中相互连接的确定方式是该事态的结构。
2.033 形式是结构的可能性。
2.034 一个事实的结构由事态的结构组成。
2.04 现存事态的总和就是世界。
2.05 现存事态的总和也决定了哪些事态不存在。
2.06 事态的存在与非存在是实在(reality)。(我们称事态的存在为正面事实,称它们的非存在为负面事实)。
2.061 事态彼此独立。
2.062 从一个事态的存在或非存在中,不可能推断出另一个事态的存在或非存在。
2.063 实在的总和就是世界。
2.1 我们将事实描绘(picture)给我们自己看。
2.11 一张图景呈现出逻辑空间中的一个情境,即事态的存在和非存在。
2.12 一张图景是实在的一个模型。
2.13 在一张图景中,客体有图景的元素与之对应。
2.131 在一张图景中,图景的元素是客体的代表。
2.14 构成一张图景的是它的元素以确定的方式相互关联。
2.141 一张图景是一个事实。
2.15 图景的元素以确定的方式相互关联这一事实,表征了事物以相同的方式相互关联。让我们称这种元素之间的关联为图景的结构,并称这种结构的可能性为图景的图示形式(pictorial form)。
2.151 图示形式是事物以与图景元素相同的方式相互关联的可能性。
2.1511 这就是图景附着于实在的方式;它一直延伸到实在。
2.1512 它像一把尺子一样靠在实在上。
2.15121 只有刻度线的端点真正触及到要测量的客体。
2.1514 因此,以这种方式构想的图景,也包含了图示关系,正是这种关系使其成为一张图景。
2.1515 这些关联,可以说是图景元素的触角,图景正是用它们接触实在。
2.16 如果一个事实要成为一张图景,它就必须与它所描绘的事物有共同之处。
2.161 图景与它所描绘的事物之间必须有某种相同之处,才能使前者成为后者的图景。
2.17 一张图景为了能够以它所做的方式——正确地或不正确地——描绘实在,它必须与实在共同拥有的是其图示形式。
2.171 一张图景可以描绘任何具有其形式的实在。一个空间图景可以描绘任何空间的东西,一个彩色的图景可以描绘任何彩色的东西,等等。
2.172 然而,一张图景不能描绘其图示形式:它展示(display)了它。
2.173 一张图景从其主体之外的位置来表征其主体。(它的立场是它的表征形式)。这就是一张图景正确地或不正确地表征其主体的原因。
2.174 然而,一张图景不能将自己置于其表征形式之外。
2.18 任何图景,无论其形式如何,为了能够以任何方式——正确地或不正确地——描绘实在,它必须与实在共同拥有的是逻辑形式,即实在的形式。
2.181 其图示形式是逻辑形式的图景称为逻辑图景。
2.182 每一张图景同时也是一张逻辑图景。(另一方面,并非每一张图景都是,例如,一张空间图景)。
2.19 逻辑图景可以描绘世界。
2.2 一张图景与它所描绘的事物拥有共同的逻辑-图示形式。
2.201 一张图景通过表征事态存在和非存在的一种可能性来描绘实在。
2.202 一张图景包含了它所表征的情境的可能性。
2.203 一张图景与实在相符或不相符;它是正确的或不正确的,是真的或假的。
2.22 一张图景表征了什么,是独立于其真假性的,通过其图示形式来实现的。
2.221 一张图景所表征的是它的意义(sense)。
2.222 它的意义与实在的相符或不相符构成了它的真或假。
2.223 为了判断一张图景是真的还是假的,我们必须将其与实在进行比较。
2.224 仅凭图景本身不可能判断它是真是假。
2.225 没有先验(a priori)为真的图景。
3. 事实的逻辑图景是一个思想(thought)。
3.001 “一个事态是可思议的”:这意味着我们可以将它描绘给我们自己看。
3.01 所有真思想的总和是世界的图景。
3.02 一个思想包含着它所思及的情境的可能性。可思议的东西也是可能的。
3.03 思想永远不可能想到任何不合逻辑的东西,因为如果可以,我们就必须以不合逻辑的方式思考。
3.031 过去人们常说,上帝可以创造除了违背逻辑规律之外的任何东西。事实是,我们无法说出一个“不合逻辑的”世界会是什么样子。
3.032 在语言中表征任何“与逻辑矛盾”的东西,就像在几何学中用坐标表征一个与空间规律矛盾的图形,或给出不存在的点的坐标一样,是不可能的。
3.0321 尽管我们可以从空间上表征一个会违反物理学规律的事态,但一个会违反几何学规律的事态则不能。
3.04 如果一个思想是先验正确的,那么它将是一个其可能性确保其真理性的思想。
3.05 只有当一个思想的真理性可以仅凭思想本身(而无需与其他任何东西进行比较)而被认识时,关于该思想为真的先验知识才可能是可能的。
3.1 在一个命题中,一个思想找到了可以通过感官感知到的表达。
3.11 我们使用一个命题的可感知符号(口头的或书面的,等等)作为一种可能情境的投射。投射的方法是思考命题的意义。
3.12 我把我们用以表达思想的符号称为命题符号。而一个命题,是处于其对世界的投射关系中的命题符号。
3.13 因此,一个命题实际上并不包含它的意义,但它包含了表达其意义的可能性。(“命题的内容”指的是有意义的命题的内容)。一个命题包含其意义的形式,但不包含其意义的内容。
3.14 构成命题符号的是它的元素(词语)以确定的方式相互关联。一个命题符号是一个事实。
3.141 一个命题不是词语的混合物。(正如音乐中的一个主题不是音符的混合物一样)。一个命题是清晰可辨的。
3.142 只有事实才能表达意义,一组名称不能。
3.143 尽管命题符号是一个事实,但这种事实被通常的书面或印刷表达形式所掩盖。例如,在印刷的命题中,命题符号和一个词语之间没有明显的本质区别。(这就是为什么弗雷格可以将一个命题称为一个复合名称)。
3.1431 如果我们想象一个由空间客体(如桌子、椅子和书籍)而非书面符号组成的命题符号,那么命题符号的本质就会非常清楚地显现出来。
3.1432 我们不应该写成:“复合符号‘aRb’说 a 与 b 处于关系 R 中”,而应该写成:“‘a’与‘b’处于某种确定的关系中这一事实,说 aRb”。
3.144 情境可以被描述,但不能被命名。
3.2 在一个命题中,思想可以这样表达:命题符号的元素与思想的客体相对应。
3.201 我称这些元素为“简单符号”,称这样的命题为“完全分析的”。
3.202 在命题中使用的简单符号称为名称。
3.203 一个名称意指一个客体。客体是它的意义。(‘A’与‘A’是相同的符号)。
3.21 情境中客体的配置对应于命题符号中简单符号的配置。
3.221 客体只能被命名。符号是它们的代表。我只能谈论它们:我不能用语言表达它们。命题只能说事物如何存在,不能说事物是什么。
3.23 要求简单符号是可能的,就是要求意义是确定的。
3.24 关于复合体的命题与关于复合体构成要素的命题处于一种内部关系中。一个复合体只能通过它的描述来给出,这种描述可能是对的,也可能是错的。一个提到复合体的命题,如果该复合体不存在,它并不会是无意义的,而只是假的。当一个命题元素意指一个复合体时,这可以从它所出现的命题中的不确定性中看出来。在这种情况下,我们知道该命题遗留了一些未确定的东西。(事实上,普遍性的符号包含一个原型)。将复合体符号缩减为一个简单符号可以藉由定义来表达。
3.25 一个命题不能通过定义被进一步分解:它是一个原始符号。
3.261 每一个有定义的符号都通过那些用于定义它的符号来意指;定义指明了道路。如果一个符号是原始的,而另一个是通过原始符号定义的,那么它们不能以相同的方式意指。名称不能通过定义来解析。(任何独立地、自身拥有意义的符号也不能被解析)。
3.262 符号未能表达的东西,它们的应用(application)显示了出来。符号所含糊带过(slur over)的东西,它们的应用清楚地表达了出来。
3.263 原始符号的意义可以通过阐明(elucidations)来解释。阐明是那些在这些符号的意义已被知晓时才被理解的命题。
3.3 只有命题才有意义;一个名称只有在命题的关联(nexus)中才有意义。
3.31 我称命题中表征其意义的任何部分为一个表达式(expression,或一个符号/symbol)。(一个命题本身就是一个表达式)。命题彼此之间可能拥有的、对其意义而言本质性的所有共同之处,就是一个表达式。一个表达式是形式和内容的一个标记。
3.311 一个表达式预设了它可能出现在其中的所有命题的形式。它是某一类命题的共同特征标记。
3.312 因此,它通过它所表征的命题的一般形式来呈现。事实上,在这种形式中,表达式将是恒定的,而其他一切都是可变的。
3.313 因此,一个表达式是通过一个变量来呈现的,该变量的值是包含该表达式的命题。(在限制情况下,变量变成一个常量,表达式变成一个命题)。我称这样的变量为“命题变量”。
3.314 一个表达式只有在一个命题中才有意义。所有变量都可以被解释为命题变量。(甚至是变量名称)。
3.315 如果我们将一个命题的构成要素变成一个变量,就会有一类命题,所有这些命题都是由此产生的变量命题的值。通常情况下,这一类命题也将取决于我们任意约定赋予原始命题某些部分的意义。但如果其中所有具有任意确定的意义的符号都被转化为变量,我们仍然会得到这样一类命题。然而,这一类命题不依赖于任何约定,而仅依赖于命题的本质。它对应于一种逻辑形式——一个逻辑原型。
3.316 一个命题变量可以取什么值是预先规定的。对值的规定就是变量。
3.317 为一个命题变量规定值,就是给出那些以该变量为共同特征的命题。这种规定是对这些命题的一种描述。因此,这种规定将只涉及符号,而不涉及它们的意义。对命题的描述是如何产生的,这一点并不重要。这种规定的唯一本质是它仅仅是对符号的描述,并没有说明所意指的内容。
3.318 像弗雷格和罗素一样,我将一个命题解释为其中所包含表达式的一个函数。
3.32 一个符号(sign)是符号(symbol)中可感知的部分。
3.321 因此,同一个符号(书面的或口头的,等等)可以被两个不同的符号(symbol)所共有——在这种情况下,它们将以不同的方式意指。
3.322 我们使用相同的符号来意指两个不同的客体,绝不能表明两者之间有一个共同的特征,如果我们以两种不同的意指模式来使用它。因为这个符号当然是任意的。所以我们可以选择两个不同的符号来代替,那么在意指的一方还会剩下什么共同之处呢?。
3.323 在日常语言中,同一个词语拥有不同的意指模式——从而属于不同的符号——或者两个拥有不同意指模式的词语在表面上以相同的方式被用于命题中,这种情况非常频繁。例如,“是”(is)一词充当系词、同一性的符号,以及存在的表达;“存在”(exist)充当一个不及物动词,如“去”(go),而“相同的”(identical)充当一个形容词;我们谈论某物(something),但也谈论某物的发生(something's happening)。(在命题“绿色是绿色的”('Green is green')中——第一个词是一个人的专名,最后一个词是一个形容词——这些词不仅有不同的意义:它们是不同的符号)。
3.324 通过这种方式,最根本的混淆很容易产生(整个哲学都充满了这些混淆)。
3.325 为了避免此类错误,我们必须使用一种符号语言,它通过不使用相同的符号表示不同的符号(symbol),以及不以表面相似的方式使用具有不同意指模式的符号,来排除这些错误:也就是说,一种由逻辑语法——逻辑句法——所支配的符号语言。(弗雷格和罗素的概念符号体系就是这样一种语言,尽管它确实未能排除所有错误)。
3.326 为了通过一个符号(sign)来识别一个符号(symbol),我们必须观察它是如何被用于表达意义的。
3.327 一个符号(sign)只有在与其逻辑-句法上的应用结合在一起时,才能确定一种逻辑形式。 3.328 如果一个符号是无用的,它就是无意义的。这就是奥卡姆(Occam)格言的要点。(如果一切行为都好像一个符号有意义,那么它就有意义)。
3.33 在逻辑句法中,一个符号的意义绝不应该发挥作用。必须可能在不提及符号意义的情况下建立逻辑句法:只需要预设对表达式的描述。
3.331 从这个观察,我们转向罗素的“类型论”。可以看出,罗素必然是错误的,因为他在建立规则时不得不提及符号的意义。
3.332 任何命题都不能陈述关于它自身的事情,因为一个命题符号不能包含它自身(这就是“类型论”的全部内容)。
3.333 一个函数不能成为它自己的论证的原因在于,函数的符号已经包含了其论证的原型,它不能包含它自身。因为让我们假设函数 F(fx) 可以是它自己的论证:在这种情况下,将有一个命题“F(F(fx))”,其中外部函数 F 和内部函数 F 必须具有不同的意义,因为内部函数具有 O(f(x)) 的形式,而外部函数具有 Y(O(fx)) 的形式。“F”这个字母是这两个函数唯一的共同点,但字母本身不意指任何东西。如果我们用‘(do) : F(Ou) . Ou = Fu’来代替‘F(Fu)’,这一点就会立刻变得清楚。这就解决了罗素的悖论。
3.334 一旦我们知道每个单独的符号是如何意指的,逻辑句法的规则就应该不言自明。
3.34 一个命题拥有本质特征和偶然特征。偶然特征是那些由命题符号产生的特定方式所导致的特征。本质特征是那些没有它们,命题就无法表达其意义的特征。
3.341 因此,一个命题的本质特征是所有能够表达相同意义的命题所共有的东西。同理,总的来说,一个符号(symbol)的本质特征是所有能够服务于相同目的的符号所共有的东西。
3.3411 因此,可以说一个客体的真正名称是所有意指它的符号所共有的东西。这样,所有类型的组合都将证明对名称来说是非本质的。 3.342 尽管我们的符号体系中存在一些武断之处,但这一点并非武断:当我们武断地确定了一件事之后,另一件事就必然是如此。(这源于符号体系的本质)。
3.3421 某种特定的意指模式可能不重要,但它是一种可能的意指模式这一点始终很重要。在哲学中通常也是如此:个体案例一次又一次地被证明是不重要的,但每个个体案例的可能性揭示了关于世界本质的一些东西。
3.343 定义是从一种语言翻译到另一种语言的规则。任何正确的符号语言都必须能够根据这些规则翻译成任何其他语言:这就是它们共同拥有的东西。
3.344 在一个符号中意指的东西,是逻辑句法规则允许我们替代它的所有符号所共有的东西。
3.3441 例如,我们可以用以下方式表达所有真值函数符号体系的共同点:它们共同拥有的是,例如,使用‘Pp’(‘非 p’)和‘p C g’(‘p 或 g’)的符号体系可以被替代其中的任何一个。(这有助于表征如何通过特定符号体系的可能性来揭示一般性事物)。
3.3442 对复合体符号的分析也不是以武断的方式进行的,以至于每次将其纳入不同的命题中时都会有不同的解析。
3.4 一个命题确定了逻辑空间中的一个位置。这个逻辑位置的存在由其构成要素的单纯存在——由有意义的命题的存在——来保证。
3.41 带有逻辑坐标的命题符号——那就是逻辑位置。
3.411 无论在几何学还是逻辑学中,一个位置都是一种可能性:有东西可以在其中存在。
3.42 一个命题只能确定逻辑空间中的一个位置:然而,整个逻辑空间必须已由它给出。(否则,否定、逻辑和、逻辑积等将引入越来越多的新协调元素)。(围绕一张图景的逻辑脚手架决定了逻辑空间。一个命题的力量贯穿整个逻辑空间)。
3.5 一个被应用并被思考过的命题符号,就是一个思想。
4. 一个思想是一个有意义的命题。
4.001 命题的总和就是语言。
4.002 人类拥有构建能够表达任何意义的语言的能力,而无需知道每个词语是如何拥有意义或其意义是什么——正如人们说话而不知道单个声音是如何产生的一样。日常语言是人类有机体的一部分,其复杂性不亚于后者。我们不可能立即从日常语言中看出语言的逻辑是什么。语言伪装了思想。它伪装到如此程度,以至于不可能从外在的服装形式推断出其下的思想形式,因为外在的服装形式的设计目的不是为了揭示身体的形式,而是为了完全不同的目的。理解日常语言所依赖的默契约定是极其复杂的。
4.003 在哲学著作中发现的大多数命题和问题不是错误的,而是无意义的。因此,我们不能对这类问题给出任何答案,而只能指出它们是无意义的。大多数哲学家的命题和问题产生于我们未能理解我们语言的逻辑。(它们属于同一类别,就像“善比美更同一还是更不同一”这样的问题)。深奥的哲学问题实际上根本就不是问题,这并不奇怪。
4.0031 所有哲学都是“语言批判”(尽管不是毛特纳/Mauthner的意义上的)。是罗素提供了服务,表明了一个命题的表观逻辑形式不必是其真实的逻辑形式。
4.01 一个命题是实在的一张图景。一个命题是我们想象的实在的一个模型。
4.011 乍一看,一个命题——例如,印在纸上的命题——似乎不是它所关涉的实在的图景。但乍一看,书面音符似乎也不是一段音乐的图景,我们的语音记号(字母表)似乎也不是我们言语的图景。然而,这些符号语言被证明是它们所表征事物的图景,即使是在普通意义上也是如此。
4.012 显然,形如“aRb”的命题给我们的印象是一张图景。在这种情况下,符号显然是所意指之物的一个相似物。
4.013 如果我们深入理解这种图示特性的本质,我们就会看到它不会被表观上的不规则性所损害(例如,在乐谱中使用 [升号] 和 [降号])。因为即使是这些不规则性也描绘了它们意图表达的东西;只是它们以不同的方式做到这一点。
4.014 留声机唱片、音乐理念、书面音符和声波,它们彼此之间都处于相同的描绘内部关系中,这种关系也存在于语言和世界之间。它们都是根据一个共同的逻辑模式构建的。(就像童话中的两个年轻人、他们的两匹马和他们的百合花一样。它们在某种意义上都是一体的)。
4.0141 有一个通用规则,音乐家可以从中获得乐谱中的交响乐,通过它可以从留声机唱片上的凹槽中推导出交响乐,并使用第一个规则再次推导出乐谱。这就是这些看起来以完全不同的方式构建的事物之间内在相似性所在。而这个规则就是将交响乐投射到音乐符号语言中的投射定律。它是将这种语言翻译成留声机唱片语言的规则。
4.015 所有意象(imagery)、所有我们的图示表达模式的可能性都包含在描绘的逻辑之中。
4.016 为了理解一个命题的本质,我们应该考虑象形文字脚本,它描绘了它所描述的事实。而字母脚本是从它发展而来的,但没有失去描绘的本质。
4.02 我们可以从这样一个事实看出这一点:我们无需解释就理解了一个命题符号的意义。
4.021 一个命题是实在的一张图景:因为如果我理解一个命题,我就知道它所表征的情境。我理解这个命题,而无需有人向我解释它的意义。
4.022 一个命题展示(shows)它的意义。一个命题展示了如果它是真的,事物是如何存在的。而且它说它们确实是那样存在的。
4.023 一个命题必须将实在限制在两种选择:是或否。为了做到这一点,它必须完全描述实在。一个命题是对一个事态的描述。正如对一个客体的描述是通过给出其外部属性来描述它一样,一个命题是通过其内部属性来描述实在。一个命题借助逻辑脚手架构建了一个世界,因此人们可以真正地从该命题中看出,如果它是真的,一切在逻辑上是如何存在的。人们可以从一个错误的命题中得出推论。
4.024 理解一个命题意味着知道如果它是真的,是其所是的东西。(因此,人们可以理解它,而不知道它是否为真)。任何理解其构成要素的人都能理解它。
4.025 在将一种语言翻译成另一种语言时,我们不是将前者的每个命题翻译成后者的一个命题,而只是翻译命题的构成要素。(并且词典翻译的不仅是名词,还有动词、形容词和连词等等;它以相同的方式对待它们)。
4.026 简单符号(词语)的意义必须向我们解释,我们才能理解它们。然而,对于命题,我们是使自己被理解。
4.027 一个命题应该能够向我们传达一个新的意义,这是它的本质的一部分。
4.03 一个命题必须使用旧的表达式来传达一个新的意义。一个命题向我们传达一个情境,因此它必须与该情境本质性地连接。而这种连接正是:它是该情境的逻辑图景。一个命题只有在它是一张图景的意义上才陈述了某事。
4.031 在一个命题中,一个情境可以说是通过实验的方式构建的。我们只需说:“这个命题表征了这样一个情境”,而不是说:“这个命题有这样的意义”。
4.0311 一个名称代表一个事物,另一个名称代表另一个事物,它们相互组合。以这种方式,整个组合——就像一幅活人画(tableau vivant)一样——呈现了一个事态。
4.0312 命题的可能性基于客体以符号作为其代表的原则。我的基本思想是,“逻辑常项”(logical constants)不是代表;事实的逻辑不可能有代表。
4.032 一个命题只有在其逻辑上是清晰可辨的意义上,它才是一个情境的图景。(即使是命题“Ambulo”(我走),也是复合的:因为它的词干有不同的词尾会产生不同的意义,它的词尾有不同的词干也会如此)。
4.04 在一个命题中,必须正好有与其所表征的情境中可区分的部分一样多的可区分部分。两者必须拥有相同的逻辑(数学)多样性(multiplicity)。(比较赫兹(Hertz)的《力学》关于动态模型的部分)。
4.041 这种数学多样性当然不能成为描绘的主体。在描绘时,人们无法摆脱它。
4.0411. 例如,如果我们要用在“fx”前面加上一个附加符号来表达我们现在写作的“(x) . fx”——例如写作“Gen. fx”——那将是不够的:我们将不知道什么被普遍化了。如果我们要试图用附加符号“g”来标示它——例如写作“f(xg)”——那也将是不够的:我们将不知道普遍性符号的范围。如果我们要试图通过在论证位置引入一个标记来做到这一点——例如写作“(G,G) . F(G,G)”——那将是不够的:我们将无法建立变量的同一性。诸如此类。所有这些意指模式都是不够的,因为它们缺乏必要的数学多样性。
4.0412 基于同样的原因,唯心主义者援引“空间眼镜”来解释空间关系的看见,也是不够的,因为它无法解释这些关系的多样性。
4.05 实在与命题进行比较。
4.06 一个命题只有作为实在的图景,才可能是真或假。 4.061 不容忽视的是,一个命题拥有独立于事实的意义:否则人们很容易假设真和假是符号及其所意指之物之间地位相同的关系。在这种情况下,人们可能会说,例如,“p”以真的方式意指的东西,“Pp”以假的方式意指,等等。
4.062 难道我们不能像迄今为止使用真命题那样,使用假命题来使自己被理解吗?——只要知道它们是意指为假的。——不能!。因为如果事物以我们用一个命题来表达的某种方式存在,并且它们确实如此,那么该命题就是真的;如果通过“p”我们意指 Pp,并且事物确实如我们所意指的那样存在,那么,以新的方式解释,“p”是真的,而不是假的。
4.0621 但是,符号“p”和“Pp”可以表达同一事物,这一点很重要。因为它表明实在中没有任何东西对应于符号“P”。否定出现在一个命题中不足以表征其意义(PPp = p)。命题“p”和“Pp”具有相反的意义,但它们对应于同一个实在。
4.063 一个说明真理概念的类比:想象白纸上的一个黑点:你可以通过说明纸上的每一个点是黑是白来描述黑点的形状。一个点是黑色的事实对应于一个正面事实,一个点是白色(非黑色)的事实对应于一个负面事实。如果我指定纸上的一个点(弗雷格所说的真值),那么这对应于被提出来判断的假设,等等。但是,为了能够说一个点是黑色的还是白色的,我必须首先知道什么时候一个点被称为黑色,什么时候被称为白色:为了能够说“‘p’是真的(或假的)”,我必须确定在什么情况下我称“p”为真,通过这样做,我就确定了命题的意义。现在,这个类比失败的地方在于:即使我们不知道黑色和白色是什么,我们也可以指出纸上的一个点,但如果一个命题没有意义,就没有东西与之对应,因为它没有指称一个可能有被称为“假”或“真”的属性的事物(一个真值)。一个命题的动词不是“是真的”或“是假的”,正如弗雷格所认为的:相反,那个“是真的”的东西必须已经包含动词。
4.064 每个命题必须已经有一个意义:它不能通过肯定而被赋予意义。事实上,它的意义就是被肯定的东西。对于否定等也是如此。 4.0641 可以说,否定必须与被否定命题所确定的逻辑位置相关。否定的命题确定了一个与被否定命题的逻辑位置不同的逻辑位置。否定的命题借助被否定命题的逻辑位置来确定一个逻辑位置。因为它将其描述为位于后者的逻辑位置之外。被否定的命题可以再次被否定,这本身表明被否定的东西已经是一个命题,而不仅仅是命题的预备性事物。
4.1 命题表征事态的存在和非存在。
4.11 所有真命题的总和是整个自然科学(或自然科学的全部知识体系)。
4.111 哲学不是自然科学之一。(“哲学”这个词一定意味着某种地位在自然科学之上或之下,而非并列的东西)。
4.112 哲学旨在对思想进行逻辑澄清。哲学不是一种学说体系而是一种活动。一个哲学著作主要由阐明(elucidations)组成。哲学不产生“哲学命题”,而是产生对命题的澄清。没有哲学,思想可以说是模糊和不明确的:它的任务是使它们清晰,并赋予它们明确的界限。
4.1121 心理学与哲学的关系并不比任何其他自然科学更密切。知识论是心理学的哲学。我对符号语言的研究,难道不正是对应于哲学家过去认为对逻辑哲学至关重要的思想过程研究吗?。只是在大多数情况下,他们纠缠于非本质性的心理学研究之中,我的方法也存在类似的风险。
4.1122 达尔文的理论与哲学无关,就像任何其他自然科学假说一样。
4.113 哲学为备受争议的自然科学领域设定了界限。
4.114 它必须为可思议之物设定界限;通过这样做,也为不可思议之物设定界限。它必须通过向外延伸可思议之物来为不可思议之物设定界限。
4.115 它将通过清晰地呈现可言说之物来意指不可言说之物。
4.116 凡是可思议的,都能清晰地被思考。凡是能用语言表达的,都能清晰地表达。
4.12 命题可以表征整个实在,但它们不能表征它们为了能够表征实在而必须与实在共有的东西——即逻辑形式。为了能够表征逻辑形式,我们将不得不能够将自己置于逻辑之外,即世界之外。
4.121 命题不能表征逻辑形式:逻辑形式在命题中被反映(mirrored)出来。在语言中找到其反映的东西,语言不能表征。通过语言表达自身的东西,我们不能用语言来表达。命题展示(show)了实在的逻辑形式。它们将它显示出来。
4.1211 因此,一个命题‘fa’展示了客体 a 出现在它的意义中,两个命题‘fa’和‘ga’展示了它们都提到了相同的客体。如果两个命题相互矛盾,那么它们的结构就展示了这一点;如果其中一个命题跟随(follows from)另一个命题,情况也是如此。等等。
4.1212 能被展示的,不能被言说。
4.1213 现在,我们也理解了我们的感受:一旦我们有了一种一切都正确的符号语言,我们就已经拥有了一种正确的逻辑观点。
4.122 在某种意义上,我们可以谈论客体和事态的形式属性,或者,在事实的情况下,谈论结构属性:在相同的意义上,谈论形式关系和结构关系。(我用“内部属性”代替“结构属性”;用“内部关系”代替“结构关系”)。我引入这些表达是为了指出哲学家中普遍存在的内部关系和恰当关系(外部关系)之间的混淆根源。然而,不可能通过命题来断言这些内部属性和关系的存在:相反,这在表征相关事态并涉及相关客体的命题中显现出来。
4.1221 一个事实的内部属性也可以被称为该事实的一个特征(以我们谈论面部特征的意义为例)。 4.123 如果一个客体不具备某个属性是不可思议的,那么该属性就是内部的。(这种蓝色阴影和那种蓝色阴影,其本身就处于从浅到深的内部关系中。不可思议的是,这两个客体不处于这种关系中)。(这里“客体”一词的转换使用对应于“属性”和“关系”词语的转换使用)。
4.124 一个可能情境的内部属性的存在,不是通过一个命题来表达的:相反,它通过该命题的一个内部属性,在表征该情境的命题中表达自身。断言一个命题拥有形式属性或否认它,同样是无意义的。
4.1241 不可能通过说一个形式拥有这个属性,另一个形式拥有那个属性来区分它们:因为这预设了将任一属性归属于任一形式是有意义的。
4.125 可能情境之间内部关系的存在,通过表征它们的命题之间的内部关系在语言中表达自身。
4.1251 在这里,我们得到了对那个令人困惑的问题“所有关系是内部的还是外部的”的答案。 4.1252 我称由内部关系排序的序列为形式序列(series of forms)。数序的顺序不是由外部关系,而是由内部关系支配的。命题序列‘aRb’、‘(d : c) : aRx . xRb’、‘(d x,y) : aRx . xRy . yRb’等等也是如此。(如果 b 与 a 处于这些关系中的一个,我称 b 是 a 的后继)。
4.126 现在我们可以谈论形式概念(formal concepts),其意义与我们谈论形式属性相同。(我引入这个表达是为了指出形式概念和恰当概念之间的混淆根源,这种混淆渗透了整个传统逻辑)。当某物作为其客体之一落入一个形式概念之下时,这不能通过一个命题来表达。相反,它体现在该客体的符号本身中。(一个名称显示它意指一个客体,一个数字的符号显示它意指一个数字,等等)。事实上,形式概念不能像恰当概念那样通过函数来表征。因为它们的特征——形式属性——不是通过函数来表达的。形式属性的表达式是某些符号的一个特征。因此,形式概念的特征符号是所有其意义落入该概念之下的符号的一个区别特征。因此,形式概念的表达式是一个命题变量,其中只有这个区别特征是恒定的。
4.127 命题变量意指形式概念,而它的值意指落入该概念之下的客体。
4.1271 每个变量都是一个形式概念的符号。因为每个变量都表征一个恒定的形式,所有它的值都拥有这个形式,这可以被视为这些值的一种形式属性。
4.1272 因此,变量名称‘x’是伪概念“客体”(object)的恰当符号。无论何时“客体”(‘object’)(“事物”/‘thing’,等等)这个词被正确使用,它都在概念符号体系中被一个变量名称表达。例如,在命题“有两个客体,它们...”中,它被表达为‘(dx,y) ... ’。无论何时它以不同的方式使用,即作为一个恰当的概念词,结果都是无意义的伪命题。因此,人们不能说,例如,“有客体”,就像人们说“有书”一样。说“有 100 个客体”或“有 10 个客体”也同样是不可能的。谈论客体总数是无意义的。这同样适用于词语“复合体”、“事实”、“函数”、“数字”等等。它们都意指形式概念,并且在概念符号体系中由变量来表征,而不是由函数或类(正如弗雷格和罗素所相信的)来表征。“1 是一个数字”、“只有一个零”以及所有相似的表达都是无意义的。(说“只有一个 1”与说“2 + 2 在 3 点钟等于 4”一样无意义)。
4.12721 形式概念在任何落入其下的客体被给出时,就立即被给出了。因此,不可能将属于一个形式概念的客体和形式概念本身作为原始观念引入。因此,例如,不可能像罗素那样,将函数的概念和特定的函数都作为原始观念引入;或将数字的概念和特定的数字都引入。
4.1273 如果我们想在概念符号体系中表达一般命题“b 是 a 的后继”,那么我们需要一个表达式来表示形式序列‘aRb’、‘(d : c) : aRx . xRb’、‘(d x,y) : aRx . xRy . yRb’、... 的通项。为了表达一个形式序列的通项,我们必须使用一个变量,因为“该形式序列的项”这个概念是一个形式概念。(这是弗雷格和罗素所忽略的:因此,他们想要表达像上面这样的一般命题的方式是不正确的;它包含一个恶性循环)。我们可以通过给出其第一项和产生下一项的运算的一般形式来确定一个形式序列的通项。
4.1274 问一个形式概念是否存在是无意义的。因为任何命题都不能作为这个问题的答案。(因此,例如,“是否存在不可分析的主谓命题?”这个问题不能被提出)。
4.128 逻辑形式是无数的。因此,在逻辑中没有优越的数字,因此也不可能存在哲学的一元论或二元论等。
4.2 一个命题的意义是它与事态存在和非存在的可能性的相符和不相符。
4.21 最简单的命题,一个基本命题(elementary proposition),断言一个事态的存在。
逻辑哲学论 作者:路德维希·维特根斯坦 16。
4.211 一个命题是基本命题的标志是:不可能有与它矛盾的基本命题。
4.22 一个基本命题由名称组成。它是名称的关联(nexus),一种连接(concatenation)。
4.221 显然,对命题的分析必须将我们引向由名称直接组合而成的基本命题。这就提出了这种组合如何形成命题的问题。
4.2211 即使世界无限复杂,以至于每个事实由无限多的事态组成,每个事态由无限多的客体组成,仍然必须存在客体和事态。
4.23 一个名称只有在一个基本命题的关联中才出现在一个命题中。
4.24 名称是简单的符号:我用单个字母(‘x’、‘y’、‘z’)来指代它们。我将基本命题写成名称的函数,因此它们具有‘fx’、‘O (x,y)’等形式。或者我用字母‘p’、‘q’、‘r’来指代它们。
4.241 当我使用两个具有相同意义的符号时,我通过在它们之间放置符号‘=’来表达这一点。“a = b”的意思是符号“b”可以替换符号“a”。(如果我使用一个等式来引入一个新符号“b”,规定它将作为已知符号 a 的替代品,那么,像罗素一样,我以‘a = b Def.’的形式写下这个等式——定义。一个定义是处理符号的规则)。
4.242 因此,形式为“a = b”的表达式仅仅是表征手段。它们没有陈述关于符号“a”和“b”的意义的任何事情。
4.243 我们能否在不知道两个名称是否意指同一事物或两个不同事物的情况下理解它们?——我们能否在不知道一个命题中出现的两个名称的意义是相同还是不同时理解它?。假设我知道一个英语单词和一个意指相同事物的德语单词的意义:那么我不可能不知道它们意指相同的事物;我必须能够将一个翻译成另一个。像‘a = a’这样的表达式,以及从中派生出来的表达式,既不是基本命题,也没有其他方式拥有意义。(这将在后面变得清楚)。
4.25 如果一个基本命题是真的,那么事态存在:如果一个基本命题是假的,那么事态不存在。
4.26 如果所有真的基本命题都被给出,结果就是对世界的完整描述。世界是通过给出所有基本命题,并补充说明其中哪些是真的哪些是假的来完全描述的。对于 n 个事态,存在着 2n 种存在和非存在的可能性。在这些事态中,任何组合都可以存在,而其余的不存在。
4.28 对应于这些组合,存在着相同数量的真-假的可能性——对于 n 个基本命题来说。
4.3 基本命题的真值可能性意味着事态存在和非存在的可能性。
4.31 我们可以通过以下类型的图式来表征真值可能性(‘T’表示‘真’,‘F’表示‘假’;在基本命题行下面的‘T’和‘F’的行以一种容易理解的方式象征着它们的真值可能性):
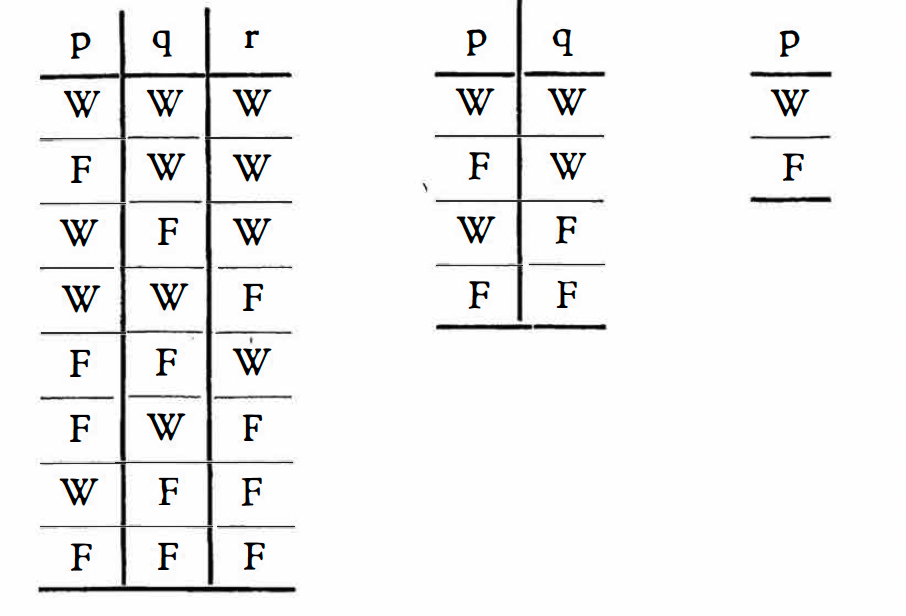
4.4 一个命题是与基本命题的真值可能性的相符和不相符的表达。
4.41 基本命题的真值可能性是命题真假性的条件。
4.411 引入基本命题为理解所有其他类型命题提供了基础,这一点立刻显得很有可能。事实上,对普遍命题的理解明显依赖于对基本命题的理解。
4.42 对于 n 个基本命题,一个命题有 22n 种方式可以与它们的真值可能性相符和不相符。
4.43 我们可以通过在图式中将标记‘T’(真)与真值可能性相关联来表达相符。缺少此标记意味着不相符。
4.431 与基本命题真值可能性的相符和不相符的表达,表达了一个命题的真值条件。一个命题是其真值条件的表达式。(因此,弗雷格在解释他的概念符号体系时,以它们作为起点是完全正确的。但是弗雷格给出的真理概念的解释是错误的:如果“真”和“假”真的是客体,并且是 Pp 等中的论证,那么弗雷格确定‘Pp’意义的方法将使其完全不确定)。
4.44 将标记‘T’与真值可能性相关联所产生的符号是一个命题符号。
4.441 很清楚,由符号‘F’和‘T’组成的复合体没有客体(或客体复合体)与之对应,就像没有东西对应于水平线和垂直线或括号一样。——没有“逻辑客体”。当然,这同样适用于表达‘T’和‘F’图式所表达的一切符号。
4.442 例如,以下是一个命题符号:
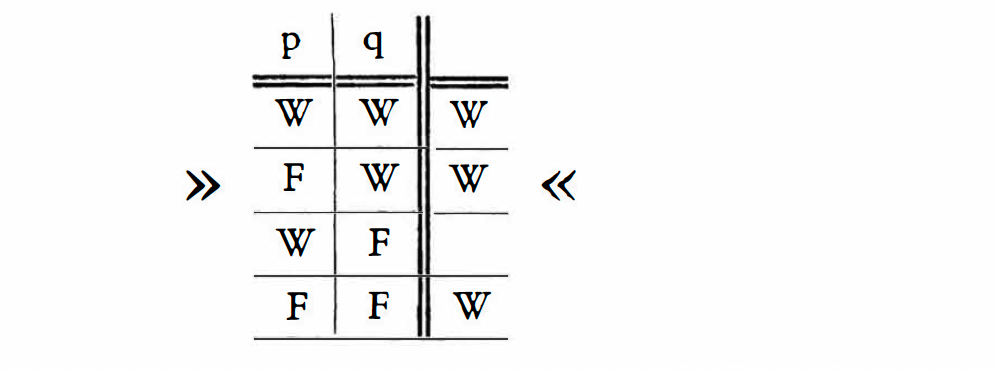
(弗雷格的“判断横线”‘|-’在逻辑上是完全无意义的:在弗雷格(和罗素)的著作中,它仅表示这些作者认为标有此符号的命题为真。因此,‘|-’不像命题的编号那样,是命题的一个组成部分。一个命题要陈述它自身为真,是完全不可能的)。如果图式中真值可能性的顺序是通过组合规则一劳永逸地固定的,那么仅凭最后一列就可以表达真值条件。如果我们现在将这一列写成一行,命题符号将变成‘(TT-T) (p,q)’或更明确地‘(TTFT) (p,q)’。(左边括号中的位置数由右边括号中的项数决定)。
4.45 对于 n 个基本命题,存在 Ln 种可能的真值条件组。可以从给定数量的基本命题的真值可能性中获得的真值条件组可以排列成一个序列。
4.46 在可能的真值条件组中,有两个极端情况。在其中一种情况下,命题对于所有基本命题的真值可能性都是真的。我们说真值条件是同义反复的(tautological)。在第二种情况下,命题对于所有真值可能性都是假的:真值条件是矛盾的(contradictory)。在前一种情况下,我们称该命题为同义反复(tautology);在后一种情况下,我们称之为矛盾(contradiction)。
4.461 命题说出它们所说的事情;同义反复和矛盾表明它们什么也没说。一个同义反复没有真值条件,因为它是无条件为真的:而一个矛盾在任何条件下都不是真的。同义反复和矛盾缺乏意义(sense)。(就像一个点,两支箭从中向相反方向射出)。(例如,当我得知外面要么下雨要么不下雨时,我对天气一无所知)。
4.46211 然而,同义反复和矛盾并不是无意义的(nonsensical)。它们是符号系统的一部分,就像‘0’是算术符号系统的一部分一样。
4.462 同义反复和矛盾不是实在的图景。它们不表征任何可能的情境。因为前者允许所有可能的情境,而后者不允许任何情境。在一个同义反复中,与世界相符的条件——表征关系——相互抵消,因此它不与实在处于任何表征关系中。
4.463 一个命题的真值条件决定了它留给事实的范围。(一个命题、一张图景或一个模型,在否定意义上,就像一个限制其他物体自由移动的固体,而在肯定意义上,就像一个被固体物质界定、其中有空间容纳一个物体的空间)。一个同义反复将整个逻辑空间——无限的整体——留给实在:一个矛盾占据了整个逻辑空间,没有给实在留下任何一点。因此,它们都不能以任何方式确定实在。
4.464 同义反复的真理性是确定的(certain),命题的真理性是可能的(possible),矛盾的真理性是不可能的(impossible)。(确定、可能、不可能:这里我们有了概率论所需的尺度的最初迹象)。 4.465 一个同义反复与一个命题的逻辑积所说的与该命题所说的相同。因此,这个积与该命题是同一的。因为不可能改变一个符号的本质部分而不改变它的意义。
4.466 对应于符号的确定逻辑组合的是它们意义的确定逻辑组合。只有对于未组合的符号,绝对任何组合都对应。换句话说,对每种情境都为真的命题根本就不能是符号的组合,因为如果它们是组合,那么只有确定的客体组合才能与之对应。(而那些非逻辑组合的,没有客体组合与之对应)。同义反复和矛盾是组合的极限情况——甚至是组合的瓦解。
4.4661 诚然,即使在同义反复和矛盾中,符号仍然相互组合——即它们彼此处于某些关系中:但这些关系没有意义,它们对符号来说是非本质的。
4.5 现在看来可以给出最一般的命题形式:也就是说,以这样一种方式描述任何符号语言的命题,使得每个可能的意义都可以通过满足该描述的符号来表达,并且每个满足该描述的符号都可以表达一个意义,只要名称的意义被适当选择。很清楚,只有对最一般的命题形式来说是本质性的东西,才可能包含在其描述中——否则它就不会是最一般的形式。一般命题形式的存在由这样一个事实证明:不可能有一个其形式无法预见(即构建)的命题。一个命题的一般形式是:事物就是这样存在的(This is how things stand)。
4.51 假设所有基本命题都已给我:那么我可以简单地问,我可以用它们构建出什么命题。在那里,我就拥有了所有命题,这就确定了它们的界限。
4.52 命题包括所有从所有基本命题的总和(当然,以及从它是全部基本命题的总和这一事实)中推导出来的一切。(因此,在某种意义上,可以说所有命题都是基本命题的概括)。
4.53 一般命题形式是一个变量。
5. 一个命题是基本命题的一个真值函数。(一个基本命题是它自身的真值函数)。
5.01 基本命题是命题的真值论证。
5.02 函数的论证很容易与名称的附加符号(affixes)相混淆。因为论证和附加符号都使我能够识别包含它们的符号的意义。例如,当罗素写‘+c’时,‘c’是一个附加符号,它表明整个符号是基数(cardinal numbers)的加法符号。但这个符号的使用是武断约定的结果,完全可以用一个简单符号代替‘+c’;然而,在‘Pp’中,‘p’不是一个附加符号而是一个论证:除非‘p’的意义已经被理解,否则‘Pp’的意义就无法被理解。(在名称“尤利乌斯·凯撒”(Julius Caesar)中,“尤利乌斯”(Julius)是一个附加符号。附加符号始终是附加给其名称的客体的描述的一部分:例如,尤利乌斯氏族的凯撒)。如果我没有理解错的话,弗雷格关于命题和函数意义的理论是基于论证和附加符号之间的混淆。弗雷格将逻辑命题视为名称,将其论证视为这些名称的附加符号。
5.1 真值函数可以排列成序列。这是概率论的基础。
5.101 给定数量的基本命题的真值函数总可以按以下类型的图式列出:

(T T T T)(p, q) 同义反复 (如果 p 则 p,如果 q 则 q。) (p z p . q z q)
(F T T T)(p, q) 用文字表达:并非 p 且 q 皆真。(P(p . q))
(T F T T)(p, q) " : 如果 q 则 p。 (q z p)
(T T F T)(p, q) " : 如果 p 则 q。 (p z q)
(T T T F)(p, q) " : p 或 q。 (p C q)
(F F T T)(p, q) " : 非 q。 (Pq)
(F T F T)(p, q) " : 非 p。 (Pp)
(F T T F)(p, q) " : p 或 q,但非两者皆真。 (p . Pq : C : q . Pp)
(T F F T)(p, q) " : 如果 p 则 p,如果 q 则 p。 (p + q)
(T F T F)(p, q) " : p
(T T F F)(p, q) " : q
(F F F T)(p, q) " : 既非 p 也非 q。 (Pp . Pq or p | q)
(F F T F)(p, q) " : p 且非 q。 (p . Pq)
(F T F F)(p, q) " : q 且非 p。 (q . Pp)
(T F F F)(p,q) " : q 且 p。 (q . p)
(F F F F)(p, q) 矛盾 (p 且非 p,且 q 且非 q。) (p . Pp . q . Pq) 我将一个命题的真值根据(truth-grounds)命名为使其为真的其真值论证的真值可能性。
5.11 如果一些命题共有的所有真值根据,同时也是某个特定命题的真值根据,那么我们说那个命题的真理性跟随(follows from)其他命题的真理性。
5.12 特别是,如果命题‘q’的所有真值根据都是命题‘p’的真值根据,那么命题‘p’的真理性就跟随命题‘q’的真理性。
5.121 一个命题的真值根据包含在另一个命题的真值根据之中:p 跟随 q。
5.122 如果 p 跟随 q,那么‘p’的意义包含在‘q’的意义之中。
5.123 如果一位神创造了一个世界,其中某些命题是真的,那么通过这个行为,祂也创造了一个所有跟随这些命题的命题都成真的世界。同样地,祂不可能创造一个命题‘p’为真的世界,而不同时创造它的所有客体。
5.124 一个命题肯定所有跟随它的命题。
5.1241 ‘p . q’是肯定‘p’的命题之一,同时也是肯定‘q’的命题之一。如果不存在一个有意义的命题同时肯定它们,那么两个命题就相互对立。每一个与另一个命题矛盾的命题都否定它。
5.13 当一个命题的真理性跟随其他命题的真理性时,我们可以从命题的结构中看出这一点。
5.131 如果一个命题的真理性跟随其他命题的真理性,这体现在命题形式彼此所处的关 逻辑哲学论 作者:路德维希·维特根斯坦 20。 系中:我们没有必要通过将它们组合在一个单一命题中来建立它们之间的这些关系;相反,这些关系是内部的,它们的存在是命题存在的直接结果。
5.1311 当我们从 p C q 和 Pp 推理 q 时,‘p C q’和‘Pp’的命题形式之间的关系在这种情况下被我们的意指模式所掩盖。但是,如果用‘p|q . | . p|q’代替‘p C q’,用‘p|p’代替‘Pp’(p|q = 既非 p 也非 q),那么内部连接就变得明显。(从 (x) . fx 推理 fa 的可能性表明,符号 (x) . fx 本身具有普遍性)。
5.132 如果 p 跟随 q,我可以从 q 推理到 p,从 q 演绎出 p。推理的性质只能从这两个命题中得出。它们本身就是推理的唯一可能证明。像弗雷格和罗素著作中那样,旨在证明推理正确的“推理定律”,是没有意义的,而且是多余的。
5.133 所有演绎都是先验地做出的。
5.134 一个基本命题不能从另一个基本命题中演绎出来。
5.135 不可能以任何方式从一个情境的存在推断出另一个完全不同的情境的存在。
5.136 没有因果关联来证明这种推论的正确性。
5.1361 我们不能从现在发生的事件推断出未来发生的事件。对因果关联的信仰是迷信。
5.1362 意志的自由在于无法预知将来发生的行动。我们只有在因果性像逻辑推理的必然性那样是一种内在必然性时,才能预知它们。——知识与被知事物之间的关联是逻辑必然性的关联。(“A 知道 p 是事实”是没有意义的,如果 p 是一个同义反复)。
5.1363 如果一个命题的真理性不跟随于它对我们来说是自明的这一事实,那么它的自明性绝不能证明我们对它真理性的信仰是正确的。
5.14 如果一个命题跟随于另一个命题,那么后者说得比前者多,而前者说得比后者少。
5.141 如果 p 跟随 q,且 q 跟随 p,那么它们是同一个命题。
5.142 一个同义反复跟随于所有命题:它什么也没说。
5.143 矛盾是命题的共同因素,但任何命题都不与其他命题共有。同义反复是所有彼此之间没有任何共同点的命题的共同因素。可以说,矛盾在所有命题之外消失:同义反复在所有命题之内消失。矛盾是命题的外部界限:同义反复是它们中心处的非实质点。
5.15 如果 Tr 是命题‘r’的真值根据的数量,如果 Trs 是命题‘s’的真值根据中同时也是‘r’的真值根据的数量,那么我们称比率 Trs : Tr 为命题‘r’赋予命题‘s’的概率程度。
5.151 在像上面 5.101 中的图式中,设 Tr 是命题 r 中‘T’的数量,设 Trs 是命题 s 中与命题 r 具有‘T’的列中的‘T’的数量。那么命题 r 赋予命题 s 的概率是 Trs : Tr。
5.1511 概率命题没有特有的特殊客体。
5.152 当命题彼此之间没有共同的真值论证时,我们称它们彼此独立。两个基本命题互相赋予 1/2 的概率。如果 p 跟随 q,那么命题‘q’赋予命题‘p’的概率是 1。逻辑推理的确定性是概率的一个限制情况。(将此应用于同义反复和矛盾)。
5.153 命题本身既不可能是或然的,也不可能是不或然的。一个事件要么发生,要么不发生:没有中间道路。 5.154 假设一个瓮中装有数量相等的黑球和白球(没有其他种类的球)。我一个接一个地取出球,然后放回瓮中。通过这个实验,我可以确定取出的黑球数量和白球数量随着抽取的进行而趋近。所以这不是一个数学真理。现在,如果我说:“我取出白球的概率等于我取出黑球的概率”,这意味着我所知道的所有情况(包括被假定为假说的自然规律)赋予一个事件发生的概率不大于另一个事件发生的概率。也就是说,根据上述定义,它们各自赋予的概率是 1/2。我通过实验确认的是,这两个事件的发生独立于我没有更详细了解的情况。
5.155 概率命题的最小单位是:我没有进一步了解的情况,赋予一个特定事件发生的概率为这样那样的程度。 5.156 概率就是以这种方式成为一种概括。它涉及对命题形式的一般描述。我们只有在缺乏确定性时才使用概率——如果我们对一个事实的知识确实不完整,但我们确实了解它形式的某些方面。(一个命题可能是一个特定情境的不完整图景,但它始终是某个东西的完整图景)。一个概率命题是其他命题的一种摘录。
5.2 命题的结构彼此处于内部关系中。
5.21 为了突出这些内部关系,我们可以采用以下表达模式:我们可以将一个命题表征为产生它的操作的结果,该操作是以其他命题(作为该操作的基础)为基础的。
5.22 一个操作是其结果与其基础的结构之间关系的一种表达。
5.23 操作是为了从一个命题制造出另一个命题而必须对前者所做的事情。
5.231 当然,这将取决于它们的形式属性,取决于它们形式的内部相似性。
5.232 排序一个序列的内部关系等同于从一个项产生另一个项的操作。
5.233 操作不能出现在一个命题以逻辑上有意义的方式从另一个命题产生之前;即在命题的逻辑构建开始的点之前。
5.234 基本命题的真值函数是以基本命题为基础的操作的结果。(我称这些操作为真值操作)。
5.2341 p 的真值函数的意义是 p 的意义的函数。否定、逻辑加法、逻辑乘法等等都是操作。(否定颠倒了一个命题的意义)。
5.24 一个操作在一个变量中显现出来;它展示了我们如何从一种命题形式转换到另一种命题形式。它表达了形式之间的差异。(操作的基础及其结果的共同之处正是基础本身)。
5.241 一个操作不是形式的标记,而仅仅是形式之间差异的标记。
5.242 从‘p’产生‘q’的操作也从‘q’产生‘r’,依此类推。只有一种方式来表达这一点:‘p’、‘q’、‘r’等等必须是变量,它们以一般的方式表达某些形式关系。
5.25 一个操作的出现并不表征一个命题的意义。事实上,操作本身并没有做出任何陈述,只有它的结果才做出陈述,而这取决于操作的基础。(操作和函数不可相互混淆)。
5.251 一个函数不能成为它自己的论证,而一个操作可以将其自身的结果之一作为其基础。
5.252 只有通过这种方式,形式序列中从一项到另一项的步骤才是可能的(在罗素和怀特海的层级中,从一个类型到另一个类型)。(罗素和怀特海不承认这种步骤的可能性,但却反复利用了它)。
5.2521 如果一个操作被反复应用于它自身的结果,我说这是它的连续应用。(‘O’O’O’a’是操作‘O’E’对‘a’连续应用三次的结果)。在类似的意义上,我说对多个命题连续应用不止一个操作。
5.2522 因此,我使用符号‘[a, x, O'x]’表示形式序列 a, O'a, O'O'a, ... 的通项。这个带括号的表达式是一个变量:带括号表达式的第一项是形式序列的开始,第二项是从序列中任意选择的项 x 的形式,第三项是序列中紧跟在 x 之后的项的形式。
5.2523 连续应用一个操作的概念等同于“依此类推”的概念。
5.253 一个操作可以抵消另一个操作的效果。操作可以相互抵消。
5.254 一个操作可以消失(例如,‘PPp’中的否定:PPp = p)。
5.3 所有命题都是基本命题上的真值操作的结果。一个真值操作是真值函数由基本命题产生的方式。真值操作的本质是,正如基本命题产生了它们自身的真值函数一样,真值函数也以相同的方式产生了进一步的真值函数。当一个真值操作应用于基本命题的真值函数时,它总是产生另一个基本命题的真值函数,即另一个命题。当一个真值操作应用于基本命题上的真值操作的结果时,总会有一个对基本命题的单一操作具有相同的结果。每个命题都是基本命题上的真值操作的结果。
5.31 4.31 中的图式即使在‘p’、‘q’、‘r’等不是基本命题时也有意义。而且很容易看出,即使‘p’和‘q’是基本命题的真值函数,4.442 中的命题符号也表达了基本命题的一个单一真值函数。
5.32 所有真值函数都是对基本命题连续应用有限次数的真值操作的结果。
5.4 至此,显而易见,没有“逻辑客体”或“逻辑常项”(在弗雷格和罗素的意义上)。
5.41 原因是,当真值操作的结果是基本命题的同一个真值函数时,它们总是相同的。
5.42 显而易见,C, z 等不是像左和右等那样的关系。弗雷格和罗素逻辑“原始符号”的相互可定义性足以表明它们不是原始符号,更不是关系的符号。很明显,通过‘P’和‘C’定义的‘z’与在‘C’的定义中与‘P’一起出现的那个‘z’是相同的;第二个‘C’与第一个是相同的;依此类推。
5.43 即使乍一看,一个事实 p 似乎会推导出无限多个其他事实(即 PPp, PPPPp, 等等),这几乎是难以置信的。逻辑(数学)的无限数量的命题从半打“原始命题”中推导出来,也同样引人注目。但事实上,所有逻辑命题都说同一件事,即什么也没说。
5.44 真值函数不是物质函数。例如,一个肯定可以通过双重否定产生:在这种情况下,是否意味着在某种意义上否定包含在肯定之中?。‘PPp’是否定 Pp,还是肯定 p——抑或是两者兼有?。命题‘PPp’不是关于否定,好像否定是一个客体:另一方面,否定的可能性已经铭写在肯定之中。如果存在一个名为‘P’的客体,那么‘PPp’所说的就会与‘p’所说的不同,正因为一个命题将是关于 P 的,而另一个则不是。
5.441 这种表观逻辑常项的消失也发生在‘P(dx) . Pfx’的情况下,它与‘(x) . fx’表达相同的意思,以及发生在‘(dx) . fx . x = a’的情况下,它与‘fa’表达相同的意思。
5.442 如果我们得到一个命题,那么与它同时得到的还有所有以它为基础的真值操作的结果。
5.45 如果存在原始逻辑符号,那么任何未能清楚显示它们彼此之间和与它们的存在理由之间的相对位置的逻辑都将是不正确的。逻辑的构造必须从其原始符号中清晰地展现出来。
5.451 如果逻辑有原始观念,它们必须彼此独立。如果引入了一个原始观念,它必须在其出现的所有组合中都被引入。因此,它不能先为一个组合引入,然后又为另一个组合重新引入。例如,一旦引入了否定,我们就必须在形如‘Pp’的命题中和像‘P(p C q)’、‘(dx) . Pfx’等命题中理解它。我们不能先为一类情况引入它,然后又为另一类情况引入它,因为那样就会留下疑问,即它在两种情况下意义是否相同,并且没有给出在两种情况下以相同方式组合符号的理由。(简而言之,弗雷格关于通过定义引入符号的言论(在他的《算术基本定律》中)也适用于原始符号的引入,尽管需要作相应的修改)。
5.452 在逻辑符号体系中引入任何新手段必然是一个重大的事件。在逻辑中,不应该以一种可以说是完全无辜的方式在括号中或脚注中引入新手段。(因此,在罗素和怀特海的《数学原理》中出现了以文字表达的定义和原始命题。为什么文字会突然出现?这需要一个证明,但没有给出,也无法给出,因为这个过程事实上是非法的)。但如果某个时刻引入新手段被证明是必要的,我们必须立即问自己:“在哪些地方这种手段的使用是不可避免的?”,并且它在逻辑中的位置必须被明确。
5.453 逻辑中的所有数字都需要证明。或者更确切地说,必须显而易见,逻辑中没有数字。没有优越的数字。
5.454 在逻辑中没有并列的地位,也不能有分类。在逻辑中,一般和特殊之间不能有区别。
5.4541 逻辑问题的解决方案必须是简单的,因为它们设定了简单的标准。人类总是有一种预感,必须存在一个领域,其中问题的答案以对称的方式先验地结合在一起——形成一个自足的系统。一个服从以下定律的领域:Simplex sigillum veri(简单性是真理的标志)。
5.46 如果我们正确地引入了逻辑符号,那么我们也应该同时引入它们所有组合的意义;即不仅是‘p C q’,还有‘P(p C q)’,等等。我们也应该同时引入所有可能括号组合的效果。因此,这将明确表明真正的通用原始符号不是‘p C q’、‘(dx) . fx’等等,而是它们组合的最一般形式。
5.461 尽管看起来不重要,但逻辑中的伪关系,如 C 和 z,需要括号——这与真正的关系不同——这实际上是很有意义的。事实上,对这些看似原始的符号使用括号本身就表明它们不是原始符号。而且没有人会相信括号具有独立的意义。
5.4611 逻辑运算的符号是标点符号。
5.47 显然,我们能先验地对所有命题形式说的任何东西,我们必须能够一下子全部说出来。一个基本命题确实在其自身中包含了所有逻辑操作。因为‘fa’与‘(dx) . fx . x = a’说的是同一件事。凡是存在复合性,就存在论证和函数,而当这些存在时,我们就已经拥有了所有逻辑常项。可以说,唯一的逻辑常项是所有命题,就其本质而言,彼此共同拥有的东西。而那就是一般命题形式。
5.471 一般命题形式是一个命题的本质。
5.4711 给出命题的本质意味着给出所有描述的本质,从而给出世界的本质。
5.472 最一般命题形式的描述就是逻辑中唯一一般原始符号的描述。
5.473 逻辑必须自理其事(Logic must look after itself)。如果一个符号是可能的,那么它也能够意指。在逻辑中,凡是可能的,都是被允许的。(“苏格拉底是相同的”之所以没有意义,是因为没有一个属性被称为“相同的”。该命题是无意义的,因为我们未能做出武断的确定,而不是因为符号本身是不合法的)。在某种意义上,我们在逻辑中不会犯错。
5.4731 罗素谈论了如此之多的自明性,在逻辑中之所以可以变得可有可无,只是因为语言本身阻止了每一个逻辑错误。使逻辑成为先验的,是不合逻辑思想的不可能性。
5.4732 我们不能给一个符号错误的意义。
5.47321 奥卡姆的格言当然不是一个武断的规则,也不是一个因其实践成功而得到证明的规则: 它的要点是符号语言中不必要的单位什么都不意指。服务于同一目的的符号在逻辑上是等价的,而没有服务于任何目的的符号在逻辑上是无意义的。
5.4733 弗雷格说,任何合法构建的命题都必须有意义。而我说,任何可能的命题都是合法构建的,如果它没有意义,那只能是因为我们未能赋予其某些构成要素意义。(即使我们认为我们已经做到了)。因此,“苏格拉底是相同的”之所以什么也没说,是因为我们没有给“相同的”(identical)这个词赋予任何形容词意义。因为当它作为一个同一性符号出现时,它以一种完全不同的方式象征——意指关系是不同的——因此,在这两种情况下,符号也是完全不同的:这两个符号只有符号(sign)是共同的,而那是一个偶然。
5.474 所必需的基本操作的数量仅取决于我们的符号体系。
5.475 所需要的只是我们应该构建一个具有特定维数——具有特定数学多样性——的符号系统。
5.476 显然,这不是一个必须被意指的原始观念数量的问题,而是一个规则的表达问题。
5.5 每个真值函数都是对基本命题连续应用操作‘(-----T)(E, ....)’的结果。这个操作否定了右边括号中的所有命题,我称之为这些命题的否定。
5.501 当一个带括号的表达式以命题作为其项时——并且括号内项的顺序是无关紧要的——我用形如‘(E)’的符号来指代它。‘(E)’是一个变量,其值是带括号表达式的项,变量上的横线表示它是括号内所有其值的代表。(例如,如果 E 有三个值 P, Q, R, 那么 (E) = (P, Q, R))。变量的值是什么,是预先规定的。这个规定是对以该变量为代表的命题的一种描述。对带括号表达式的项的描述是如何产生的,这一点并不重要。我们可以区分三种描述:1. 直接枚举,在这种情况下,我们可以简单地用作为其值的常量替换变量;2. 给出一个函数 fx,其对于 x 的所有值都是要描述的命题;3. 给出一个支配命题构建的形式法则,在这种情况下,带括号的表达式以形式序列的所有项作为其成员。
5.502 因此,我用‘N(E)’代替‘(-----T)(E, ....)’。N(E) 是命题变量 E 的所有值的否定。
5.503 显然,我们可以很容易地表达命题如何可以通过这个操作构建,以及如何不能通过它构建;因此,一定可以找到一个精确的表达来描述这一点。
5.51 如果 E 只有一个值,那么 N(E) = Pp (非 p);如果它有两个值,那么 N(E) = Pp . Pq (既非 p 也非 g)。
5.511 逻辑——包罗万象、映照世界的逻辑——如何使用如此奇特的怪癖和权宜之计?。只因为它们在一个无限精细的网格中相互连接,这面巨大的镜子。
5.512 ‘Pp’在‘p’为假时为真。因此,在命题‘Pp’中,当它为真时,‘p’是一个假命题。那么,横线‘P’如何使其与实在相符?。但在‘Pp’中,进行否定的不是‘P’,而是所有否定 p 的这种符号体系的符号所共有的东西。也就是说,支配‘Pp’、‘PPPp’、‘Pp C Pp’、‘Pp . Pp’等等(直至无限)的构建的共同规则。而这个共同因素映照了否定。
5.513 我们可以说,所有同时肯定 p 和 q 的符号所共同拥有的东西是命题‘p . q’;所有肯定 p 或 q 的符号所共同拥有的东西是命题‘p C q’。同样,我们可以说,如果两个命题彼此之间没有任何共同点,那么它们相互对立,并且每个命题只有一个否定命题,因为只有一个命题完全位于它之外。因此,在罗素的符号体系中也很明显,‘q : p C Pp’与‘q’说的是同一件事,而‘p C Pq’什么也没说。
5.514 一旦建立了一个符号体系,其中就会有一个支配所有否定 p 的命题的构建规则,一个支配所有肯定 p 的命题的构建规则,以及一个支配所有肯定 p 或 q 的命题的构建规则;依此类推。这些规则等同于符号;它们的意义在其中被反映。
5.515 必须在我们的符号中显而易见,只有命题才能通过‘C’、‘.’等等相互组合。事实确实如此,因为‘p’和‘q’中的符号本身就预设了‘C’、‘P’等等。如果‘p C q’中的符号‘p’不代表一个复合符号,那么它本身就不能有意义:但在那种情况下,具有与 p 相同意义的符号‘p C p’、‘p . p’等也必然缺乏意义。但是如果‘p C p’没有意义,那么‘p C q’也不能有意义。
5.5151 否定命题的符号必须用肯定命题的符号来构建吗?。为什么不能通过一个负面事实来表达一个否定命题?。(例如,假设“a”不与“b”处于某种关系中;那么这可能被用来表示 aRb 不是事实)。但实际上,即使在这种情况下,否定命题也是通过间接使用肯定命题来构建的。肯定命题必然预设否定命题的存在,反之亦然。
5.52 如果 E 以函数 fx 对 x 的所有值的值作为其值,那么 N(E) = P(dx) . fx。
5.521 我将所有(all)这个概念与真值函数分离。弗雷格和罗素将普遍性与逻辑积或逻辑和联系起来引入。这使得理解命题‘(dx) . fx’和‘(x) . fx’变得困难,这两个观念都嵌入其中。
5.522 普遍性符号的独特之处在于,首先,它指示一个逻辑原型,其次,它突出了常项。
5.523 普遍性符号作为一个论证出现。
5.524 如果客体被给出,那么所有客体也就同时被给出了。如果基本命题被给出,那么所有基本命题也就同时被给出了。
5.525 将命题‘(dx) . fx’用“fx 是可能的”来转述是错误的,正如罗素所做的那样。一个情境的确定性、可能性或不可能性不是由一个命题表达的,而是由一个表达式是一个同义反复、一个有意义的命题或一个矛盾来表达的。我们不断倾向于援引的先例,必须存在于符号本身之中。
5.526 我们可以通过完全概括的命题来完整地描述世界,即无需先将任何名称与特定客体关联起来。 5.5261 一个完全概括的命题,像所有其他命题一样,是复合的。(这体现在我们必须单独提及‘O’和‘s’在‘(dx, O) . Ox’中。它们都独立地与世界处于意指关系中,就像在非概括的命题中一样)。一个复合符号的标志是它与其他符号有共同之处。
5.5262 每个命题的真假确实会对世界的总体构建做出一些改变。基本命题的总和为其构建留下的范围,与完全普遍命题所划定的范围完全相同。(如果一个基本命题是真的,那至少意味着多了一个真的基本命题)。
5.53 我用符号的同一性来表达客体的同一性,而不是通过使用同一性符号。我用符号的差异来表达客体的差异。
5.5301 显而易见,同一性不是客体之间的关系。如果我们考虑例如命题‘(x) : fx . z . x = a’,这一点就变得非常清楚。这个命题所说的仅仅是只有 a 满足函数 f,而不是说只有与 a 有某种关系的事物满足该函数。当然,那时可能会说只有 a 与 a 有这种关系;但为了表达这一点,我们需要同一性符号本身。 5.5302 罗素对‘=’的定义是不充分的,因为根据它,我们不能说两个客体拥有所有共同的属性。(即使这个命题永远不正确,它仍然有意义)。
5.5303 粗略地说,说两个事物是同一的是无意义的,而说一个事物与自身是同一的则是什么也没说。 5.531 因此,我不写‘f(a, b) . a = b’,而是写‘f(a, a)’(或‘f(b, b));我不写‘f(a,b) . Pa = b’,而是写‘f(a, b)’。
5.532 同样地,我不写‘(dx, y) . f(x, y) . x = y’,而是写‘(dx) . f(x, x)’;我不写‘(dx, y) . f(x, y) . Px = y’,而是写‘(dx, y) . f(x, y)’。
5.5321 因此,例如,我们用‘(dx) . fx . z : P(dx, y) . fx. fy’代替‘(x) : fx z x = a’。命题“只有一个 x 满足 f( )”将读作‘(dx) . fx : P(dx, y) . fx . fy’。
5.533 因此,同一性符号不是概念符号体系的本质构成要素。
5.534 现在我们看到,在一个正确的概念符号体系中,像‘a = a’、‘a = b . b = c . z a = c’、‘(x) . x = x’、‘(dx) . x = a’等伪命题甚至无法被写下来。
5.535 这也解决了所有与这些伪命题相关的问题。罗素的“无穷公理”(axiom of infinity)带来的所有问题都可以在这一点上得到解决。无穷公理想要说的话,将通过具有不同意义的无限多个名称的存在在语言中表达出来。
5.5351 在某些情况下,人们会倾向于使用形如‘a = a’或‘p z p’之类的表达式。事实上,这发生在我们想要谈论原型时,例如命题、事物等等。因此,在罗素的《数学原理》中,“p 是一个命题”——这是无意义的——被赋予了符号表达‘p z p’,并作为假设放在某些命题之前,以排除其论证位置除了命题之外的一切。(将假设‘p z p’放在一个命题之前,以确保其论证具有正确的形式,是无意义的,原因在于,如果以非命题作为论证,该假设不会变成假,而是变成无意义,并且错误类型的论证会使命题本身变得无意义,因此它自我保护,避免错误论证,与附加了那个没有意义的假设一样好或一样糟)。
5.5352 以同样的方式,人们曾想通过写‘P(dx) . x = x’来表达“没有事物”。但即使这是一个命题,如果事实上“有事物”但它们与自身不相同,它难道不会同样是真的吗?。
5.54 在一般命题形式中,命题出现在其他命题中仅仅作为真值操作的基础。
5.541 乍一看,命题似乎也可能以不同的方式出现在另一个命题中。特别是在心理学中的某些命题形式中,例如“A 相信 p 是事实”和“A 有思想 p”等等。因为如果表面地考虑这些命题,看起来命题 p 与客体 A 处于某种关系中。(在现代知识论(罗素、摩尔等)中,这些命题确实是以这种方式被解释的)。
5.542 然而,很清楚,“A 相信 p”、“A 有思想 p”和“A 说 p”的结构是形如“‘p’说 p”:这不涉及事实与客体的关联,而是通过客体的关联来实现事实的关联。
5.5421 这也表明,根本没有像当今肤浅心理学中所构想的那样——灵魂、主体等等——这样的东西。事实上,一个复合的灵魂就不再是一个灵魂。
5.5422 对命题“A 做出判断 p”形式的正确解释,必须表明一个判断不可能是无意义的。(罗素的理论不满足这一要求)。
5.5423 感知一个复合体意味着感知其构成要素以这样那样的方式相互关联。这无疑也解释了为什么有两种可能的方式来看一个图形作为立方体;以及所有类似的现象。
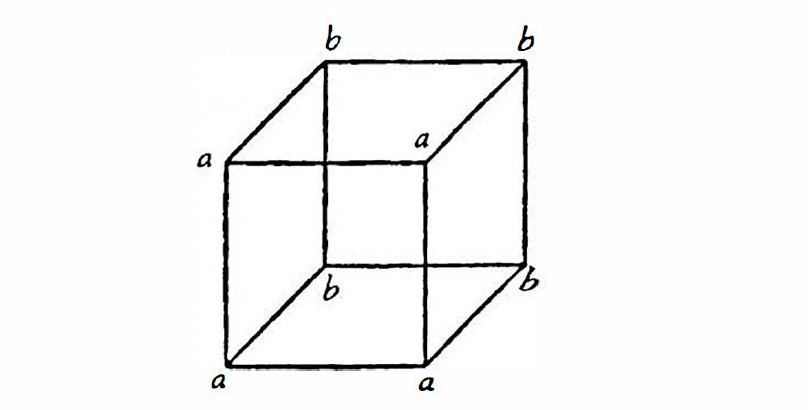
因为我们实际上看到了两个不同的事实。(如果我首先看标记为 a 的角,而只瞥一眼 b,那么 a 似乎在前面,反之亦然)。
5.55 我们现在必须先验地回答关于所有可能的基本命题形式的问题。基本命题由名称组成。然而,既然我们无法给出具有不同意义的名称的数量,我们也无法给出基本命题的构成。
5.551 我们的基本原则是:无论何时一个问题可以通过逻辑来决定,它都必须能够毫不费力地被决定。(如果我们陷入需要观察世界才能找到这类问题答案的境地,这表明我们走上了一条完全错误的道路)。
5.552 我们为了理解逻辑所需要的“经验”不是某事是事物状态的经验,而是某物存在的经验:然而,那不是一个经验。逻辑先于每一个经验——某事是如此。它先于“如何?”这个问题,而不是先于“什么?”这个问题。
5.5521 如果不是这样,我们如何应用逻辑?。我们可以这样说:如果即使没有世界,也会有逻辑,那么既然有一个世界,逻辑怎么能存在呢?。
5.553 罗素说,不同数量的事物(个体)之间存在简单的关系。但数量是多少?。这又该如何决定?——通过经验吗?。(没有优越的数字)。
5.554 给出任何特定的形式都将是完全武断的。
5.5541 应该可以先验地回答我是否会陷入需要一个 27 项关系符号来意指某事的位置。
5.5542 但问这样的问题真的合法吗?。我们可以在不知道是否有任何东西可以与之对应的情况下设置一个符号形式吗?。问“为了使某事可能发生,必须有什么?”有意义吗?。
5.555 显然,我们对基本命题有一些概念,完全独立于它们特定的逻辑形式。但当存在一个我们可以创建符号的系统时,对逻辑来说重要的是系统而不是单个符号。无论如何,在逻辑中,我真的必须处理我可以发明出来的形式吗?。我必须处理的,必然是使我能够发明它们的东西。
5.556 基本命题的形式不可能有层级结构。我们只能预见我们自己构建的东西。
5.5561 经验实在受客体总和的限制。这个限制也体现在基本命题的总和中。层级结构是,而且必须是,独立于实在的。
5.5562 如果我们纯粹基于逻辑理由知道必须存在基本命题,那么每个理解 C 形式命题的人都必须知道这一点。
5.5563 事实上,我们日常语言中的所有命题,就它们本身而言,都处于完美的逻辑秩序之中。——我们必须在这里阐述的那个完全简单的事物,不是真理的一个相似物,而是其全部的真理本身。(我们的问题不是抽象的,而是可能最具体的问题)。
5.557 逻辑的应用决定了存在哪些基本命题。属于其应用的东西,逻辑无法预料。清楚的是,逻辑绝不能与其应用发生冲突。但逻辑必须与其应用接触。因此,逻辑及其应用不能重叠。
5.5571 如果我不能先验地说出存在哪些基本命题,那么尝试这样做必然会导致明显的无意义。
5.6 我的语言的界限意味着我的世界的界限。
5.61 逻辑渗透于世界:世界的界限也是逻辑的界限。因此,我们不能在逻辑中说:“世界中有这个,有那个,但没有那个”。因为这似乎预设了我们在排除某些可能性,而这不可能是事实,因为它要求逻辑超越世界的界限;只有那样,它才能从另一侧看待那些界限。我们不能思考我们不能思考的东西;所以我们不能思考的东西,我们也无法言说。
5.62 这个论述为理解独我论(solipsism)有多少真理提供了关键。因为独我论者所意指的完全是正确的;只是它不能被言说,而是自我显现。世界是我的世界:这体现在这样一个事实中:语言的界限(我唯一理解的语言的界限)意味着我的世界的界限。
5.621 世界和生命是一体的。
5.63 我就是我的世界。(微观世界)。
5.631 没有像思考或怀有想法的主体(subject)这样的东西。如果我写一本名为《我所发现的世界》的书,我将不得不包括一份关于我身体的报告,并且不得不说明哪些部分受我的意志支配,哪些不受,等等,这是一种隔离主体的方法,或者更确切地说,是表明在重要意义上没有主体的方法;因为只有它不能在那本书中被提及。——
5.632 主体不属于世界:相反,它是世界的界限。
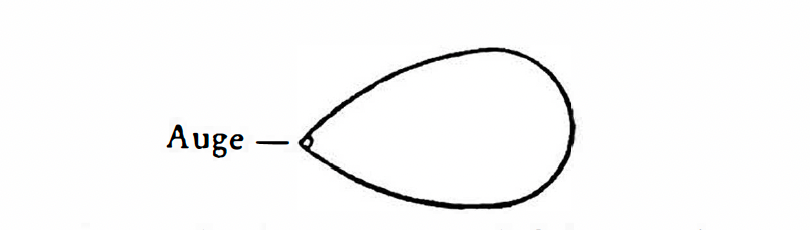
5.633 在世界中,形而上学的主体在哪里可以找到?。你会说这正像眼睛和视觉领域的情况。但你实际上没有看到眼睛。视觉领域中没有任何东西允许你推断它是被一只眼睛所看见。
5.6331 因为视觉领域的形状肯定不是这样的。
5.634 这与我们的经验没有一部分同时是先验的事实相关。我们所看到的一切都可能不同于它现在的样子。我们能描述的一切都可能不同于它现在的样子。没有事物的先验秩序。
5.64 在这里可以看出,独我论,当其蕴涵被严格推导时,与纯粹实在论重合。独我论的自我(self)缩小到一个没有延伸的点,剩下的就是与它相协调的实在。
5.641 因此,确实存在一种哲学可以以非心理学的方式谈论自我的意义。“世界是我的世界”这一事实将自我带入了哲学。哲学的自我不是人,不是心理学所处理的人类身体或人类灵魂,而是形而上学的主体,世界的界限——而非世界的一部分。
6. 一个真值函数的一般形式是 [p, E, N(E)]。这是命题的一般形式。
6.001 这所说的正是:每个命题都是对基本命题连续应用操作 N(E) 的结果。
6.002 如果给定了命题构建的一般形式,那么也就同时给定了通过一个操作可以从一个命题产生另一个命题的一般形式。
6.01 因此,一个操作 /'(n) 的一般形式是 [E, N(E)]' (n) ( = [n, E, N(E)])。这是从一个命题到另一个命题的最一般转换形式。
6.02 这就是我们如何得到数字。我给出以下定义 x=/0x Def.,′/v′x=/v+1′x Def.。因此,根据这些处理符号的规则,我们将序列 x,/′x,/′/′x,/′/′/′x,… 写成以下方式 $/{0}'x, /^{0+1}'x, /^{0+1+1}'x, /^{0+1+1+1}'x, \dots$。因此,我用‘$[/^{0}'x, /v'x, /v+1'x]$’代替‘[x, E, /'E]’。我给出以下定义 0+1=1 Def.,0+1+1=2 Def.,0+1+1+1=3 Def.(依此类推)。
6.021 一个数字是一个操作的指数。
6.022 数字的概念就是所有数字所共有的东西,即数字的一般形式。数字的概念是变量数字。而数值相等(numerical equality)的概念是所有数值相等特定情况的一般形式。
6.03 整数的一般形式是 [0,E,E+1]。
6.031 类理论在数学中是完全多余的。这与数学中所需的普遍性不是偶然的普遍性这一事实相关。
6.1 逻辑命题是同义反复(tautologies)。
6.11 因此,逻辑命题什么也没说。(它们是分析命题。)。
6.111 所有使逻辑命题看起来具有内容的理论都是错误的。例如,人们可能认为“真”和“假”这两个词意指(signified)属性中的两种属性,那么每个命题都拥有这两种属性之一就似乎是一个显著的事实。在这种理论下,这看起来一点也不明显,正如,例如,命题“所有玫瑰要么是黄色的要么是红色的”即使是真的,听起来也不会是显而易见的。事实上,逻辑命题获得了自然科学命题的所有特征,而这正是它被错误解释的明确标志。
6.112 对逻辑命题的正确解释必须赋予它们在所有命题中独特的地位。
6.113 逻辑命题的独特标志是人们可以仅凭符号本身就能认识到它们是真的,而这个事实本身就包含了整个逻辑哲学。同样,非逻辑命题的真假性不能仅凭命题本身被认识,这也是一个非常重要的事实。
6.12 逻辑命题是同义反复这一事实,展示了语言和世界的形式——逻辑——属性。一个同义反复是通过这种特定的方式连接其构成要素而产生的,这一事实表征了其构成要素的逻辑。如果命题以某种方式连接时要产生一个同义反复,它们就必须拥有某些结构属性。因此,它们以这种方式组合时产生同义反复,表明了它们拥有这些结构属性。
6.1201 例如,命题‘p’和‘Pp’在组合‘(p . Pp)’中产生一个同义反复这一事实,表明它们相互矛盾。命题‘p ⊃ q’、‘p’和‘q’以‘(p ⊃ q) . (p) :⊃: (q)’的形式相互组合时产生一个同义反复这一事实,表明 q 跟随于 p 和 p ⊃ q。‘(x) . fxx :⊃: fa’是一个同义反复这一事实,表明 fa 跟随于 (x) . fx。等等。
6.1202 显然,人们可以通过使用矛盾而非同义反复来达到相同的目的。
6.1203 为了识别一个表达式是否是同义反复,在其中没有普遍性符号(generality-sign)出现的情况下,人们可以使用以下直观方法:我用‘TpF’、‘TqF’、‘TrF’等代替‘p’、‘q’、‘r’等。我通过括号表达真值组合(Truth-combinations),例如,我使用线条来表达整个命题的真假与它的真值论证的真值组合之间的关联,方式如下:因此,例如,这个符号将代表命题 p ⊃ q。现在,举例来说,我想检验命题 P(p . Pp) (矛盾律)以确定它是否是一个同义反复。在我们的符号体系中,形式‘PE’被写为,形式‘E . η’被写为。因此,命题 P(p . Pp) 读作如下:如果我们在此用‘p’替换‘q’并检验最外层的 T 和 F 如何与最内层的 T 和 F 连接,结果将是整个命题的真与它论证的所有真值组合相关联,而它的假与任何真值组合都不相关联。
6.121 逻辑命题通过将命题组合起来以形成不陈述任何东西的命题,来演示(demonstrate)命题的逻辑属性。这种方法也可以被称为零方法(zero-method)。在一个逻辑命题中,命题彼此之间被带入平衡状态,而这种平衡状态则指示了这些命题的逻辑构成必须是什么。
6.122 由此可知,我们实际上可以没有逻辑命题;因为在一个合适的符号体系中,我们事实上可以通过仅仅检查命题本身来识别它们的形式属性。
6.1221 例如,如果两个命题‘p’和‘q’在组合‘p ⊃ q’中产生一个同义反复,那么 q 跟随于 p 是清楚的。例如,我们可以从这两个命题本身看出‘q’跟随于‘p ⊃ q . p’,但也可以用这种方式来展示它:我们将它们组合成‘p ⊃ q . p :⊃: q’,然后展示这是一个同义反复。
6.1222 这为以下问题提供了一些启发:逻辑命题不能像不能被经验驳倒一样,也不能被经验证实。一个逻辑命题不仅必须不能被任何可能的经验驳倒,而且也必须不能被任何可能的经验证实。
6.1223 现在变得清楚了,为什么人们经常觉得仿佛轮到我们去“设定”(postulate)“逻辑真理”。原因在于,我们可以在我们设定一个足够恰当的符号体系的范围内设定它们。
6.1224 现在也变得清楚了,为什么逻辑被称为形式理论和推理理论。
6.123 显然,逻辑定律不能反过来受制于逻辑定律。(罗素所认为的每种“类型”都有一个特殊的矛盾律的情况并不存在;一个定律就足够了,因为它不适用于自身)。
6.1231 逻辑命题的标记不是普遍有效性(general validity)。普遍性不过是偶然地对所有事物有效。一个非概括的命题可以像一个概括的命题一样是同义反复。
6.1232 逻辑的普遍有效性可以被称为本质的,以区别于像“所有人皆凡人”这类命题的偶然普遍有效性。像罗素的“可还原性公理”(axiom of reducibility)这样的命题不是逻辑命题,这就解释了我们的感受:即使它们是真的,它们的真也只能是幸运的偶然结果。
6.1233 可以想象一个可还原性公理不成立的世界。然而,显然逻辑与我们的世界是否真的如此无关。
6.124 逻辑命题描述了世界的脚手架(scaffolding),或者更确切地说,它们表征(represent)了它。它们没有“主题”(subject-matter)。它们预设了名称具有意义,基本命题具有意义(sense);这就是它们与世界的联系。通过某些符号组合——其本质涉及拥有一个确定的特征——是同义反复这一事实,必然指示了关于世界的一些东西。这包含了决定性的一点。我们说过,在我们使用的符号中有一些是武断的,有一些则不是。在逻辑中,只有后者才表达东西(express):但这表明逻辑不是一个我们借助符号表达我们所希望之物的领域,而是一个绝对必要符号的本质自我言说的领域。如果知道任何符号语言的逻辑句法,那么所有逻辑命题就已经被给予了。
6.125 即使根据旧的逻辑观念,也可以事先给出对所有“真”逻辑命题的描述。
6.1251 因此,逻辑中永远不会有惊喜。
6.126 人们可以通过计算符号的逻辑属性来计算一个命题是否属于逻辑。这就是我们“证明”一个逻辑命题时所做的事情。因为,我们不关心意义,我们仅使用处理符号的规则,从其他命题中构建出逻辑命题。逻辑命题的证明包括以下过程:我们通过连续应用某些操作,从其他逻辑命题中产生它们,这些操作总是从初始的同义反复中产生进一步的同义反复。(事实上,只有同义反复会跟随于一个同义反复)。当然,这种展示逻辑命题是同义反复的方式对逻辑来说并不重要,因为证明所依据的命题必须无需任何证明就显示它们是同义反复。
6.1261 在逻辑中,过程和结果是等价的。(因此没有惊喜)。
6.1262 逻辑中的证明仅仅是一种机械手段,用于简化在复杂情况下对同义反复的识别。
6.1263 确实,如果一个有意义的命题可以从其他命题中被逻辑地证明,那将是过于引人注目的,逻辑命题也是如此。从一开始就很清楚,一个有意义命题的逻辑证明和逻辑中的证明必须是两个完全不同的事情。
6.1264 一个有意义的命题陈述了某事,其证明显示了其为真。在逻辑中,每个命题都是一种证明的形式。每个逻辑命题都是以符号表示的肯定前件式(modus ponens)。(人们不能通过一个命题来表达肯定前件式)。
6.1265 总是可以以这样一种方式来解释逻辑:每个命题都是它自身的证明。
6.127 所有逻辑命题都具有同等的地位:它们并非有些是本质上派生的命题。每个同义反复都自己显示了它是一个同义反复。
6.1271 显然,“逻辑原始命题”的数量是武断的,因为人们可以从一个单一的原始命题中推导出逻辑,例如,通过简单地构建弗雷格原始命题的逻辑积。(弗雷格或许会说,那样我们就不会再有一个立即可自明的原始命题了。但令人惊讶的是,像弗雷格这样严谨的思想家竟然诉诸于自明程度作为逻辑命题的标准)。
6.13 逻辑不是一套学说体系,而是世界的镜像。逻辑是先验的(transcendental)。
6.2 数学是一种逻辑方法。数学命题是等式,因此是伪命题。
6.21 一个数学命题不表达一个思想。
6.211 事实上,在现实生活中,一个数学命题从来都不是我们想要的。相反,我们仅仅在从不属于数学的命题推论到同样不属于数学的命题时,才利用数学命题。(在哲学中,问题“我们究竟用这个词或这个命题来做什么?”会反复带来有价值的见解)。
6.22 逻辑命题通过同义反复来展示的世界逻辑,由数学通过等式来展示。
6.23 如果两个表达式通过等号符号连接,这意味着它们可以相互替换。但这必须在两个表达式本身中就显现出来,无论情况是否如此。当两个表达式可以相互替换时,这表征了它们的逻辑形式。
6.231 肯定可以被解释为双重否定,这是一个属性。‘1 + 1 + 1 + 1’可以被解释为‘(1 + 1) + (1 + 1)’,这是一个属性。
6.232 弗雷格说,这两个表达式具有相同的意义(meaning)但不同的意指(senses)。但关于一个等式的本质点在于,它对于显示通过等号连接的两个表达式具有相同意义来说并不是必需的,因为这可以从两个表达式本身看出。
6.2321 证明数学命题的可能性仅仅意味着,它们的正确性可以被感知,而无需将其所表达的内容本身与事实进行比较以确定其正确性。
6.2322 断言两个表达式的意义同一性是不可能的。因为为了能够断言任何关于它们意义的事情,我必须知道它们的意义,而我不可能在不知道它们所意指的东西是相同还是不同时知道它们的意义。
6.2323 一个等式仅仅标志着我从哪个观点来考虑这两个表达式:它标志着它们在意义上的等价性。 6.233 关于解决数学问题是否需要直觉(intuition)的问题,答案是,在这种情况下,语言本身提供了必要的直觉。 6.2331 计算过程有助于实现这种直觉。计算不是一个实验。
6.234 数学是一种逻辑方法。
6.2341 数学方法的本质特征是它使用等式。正是因为这种方法,每个数学命题都必须是不言自明的。
6.24 数学得出其等式的方法是代换(substitution)的方法。因为等式表达了两个表达式的可代换性,并且从一系列等式出发,我们通过根据这些等式代换不同的表达式,推导出新的等式。
6.241 因此,命题 2 + 2 = 4 的证明如下:(/v)n'x = /v x u'x Def.,/2 x 2'x = (/2)2'x = (/2)1 + 1'x = /2' /2'x = /1 + 1'/1 + 1'x = (/'/)'(/'/)'x = /'/'/'/'x = /1 + 1 + 1 + 1'x = /4'x。
6.3 对逻辑的探索意味着对一切受规律支配的事物的探索。而在逻辑之外,一切都是偶然的。
6.31 所谓的归纳法(induction)定律不可能是逻辑定律,因为它显然是一个有意义的命题。——因此,它也不能是一个先验定律。
6.32 因果律不是一个定律,而是定律的形式。
6.321 “因果律”——这是一个一般名称。正如在力学中,例如有“最小原理”,如最小作用量原理,同样在物理学中也有因果定律,即具有因果形式的定律。
6.3211 事实上,人们甚至在不知道“最小作用量原理”确切内容之前,就猜测到它必然存在。(在这里,如同以往一样,先验确定的东西被证明是纯粹逻辑的)。
6.33 我们不是先验地相信守恒定律,而是先验地知道一种逻辑形式的可能性。
6.34 所有这类命题,包括充足理由律、自然界的连续性定律、自然界的最小努力定律等等——所有这些都是关于科学命题可以被塑造的形式的先验见解。
6.341 例如,牛顿力学对世界的描述施加了一种统一的形式。让我们想象一个带有不规则黑点的白色表面。然后我们说,无论这些黑点形成什么样的图像,我总是可以通过用足够细密的方格网覆盖表面,然后对每个方格说它是黑色的还是白色的,来尽可能接近地描述它。通过这种方式,我就对表面的描述施加了一种统一的形式。这种形式是可选的,因为我也可以使用三角网或六边形网格来达到相同的效果。或许使用三角网会使描述更简单:也就是说,我们可能可以用一个粗糙的三角网比用一个细密的方格网更准确地描述表面(或反之),依此类推。不同的网格对应于不同的描述世界系统。力学通过规定所有用于描述世界的命题必须以给定的方式,从一组给定的命题——力学公理——中获得,从而确定了一种描述世界的形式。因此,它提供了构建科学大厦的“砖块”,并说:“无论你想建造什么样的建筑,都必须以某种方式,并且只能用这些砖块来构建”。(正如使用数字系统我们必须能够写下我们希望的任何数字一样,使用力学系统我们也必须能够写下我们希望的任何物理命题)。
6.342 现在我们可以看到逻辑和力学的相对位置。(网格也可能由不止一种网格组成:例如,我们可以同时使用三角形和六边形)。能够用给定形式的网格来描述像上面提到的那样的图像,并不能告诉我们关于图像的任何信息。(因为这适用于所有这类图像)。但是,能够通过特定尺寸的特定网格来完整描述图像,这一点确实表征了图像。同样地,能够通过牛顿力学描述世界,并不能告诉我们关于世界的任何信息:但正是能够用这些方法来描述世界的精确方式,才告诉了我们关于世界的一些信息。通过一个力学系统可以比另一个系统更简单地描述世界这一事实,也告诉了我们关于世界的一些信息。
6.343 力学是尝试根据一个单一的计划来构建所有我们描述世界所需的真命题。
6.3431 物理定律,连同它们所有的逻辑装置,仍然(无论多么间接地)是关于世界客体的言说。
6.3432 我们不应该忘记,任何通过力学对世界的描述都将是完全普遍性的。例如,它永远不会提到特定的质点:它只会谈论任何质点。
6.35 尽管我们图像中的斑点是几何图形,但几何学显然对它们的实际形式和位置什么也说不出来。然而,网格是纯粹几何的;它的所有属性都可以先验地给出。像充足理由律等定律是关于网格的,而不是关于网格所描述的东西的。
6.36 如果存在一个因果律,它可能会以以下方式表达:存在着自然定律。但这当然不能被言说:它会自我显现。
6.361 人们可能会用赫兹(Hertz)的术语说,只有受规律支配的连接才是可思议的。
6.3611 我们不能将一个过程与“时间的流逝”进行比较——因为没有这样的东西——而只能与另一个过程进行比较(例如,计时器的运作)。因此,我们只能通过依赖于某种其他过程来描述时间的流逝。完全类似的情况适用于空间:例如,当人们说两个事件(它们相互排斥)都不会发生,因为没有什么会导致一个发生而不是另一个发生时,这实际上是我们无法描述其中一个事件,除非找到了某种不对称性。如果找到了这种不对称性,我们可以将其视为导致一个事件发生而另一个事件不发生的原因。
6.36111 康德关于右手和左手不能重合的问题,甚至在二维空间中也存在。事实上,它存在于一维空间中,其中两个全等图形 a 和 b,除非被移出这个空间,否则无法重合。右手和左手实际上是完全全等的。它们不能重合是完全不相关的。如果一个右手手套可以在四维空间中被翻转,那么它可以戴在左手上。
6.362 可以被描述的东西也可以发生:而因果律想要排除的东西甚至无法被描述。
6.363 归纳的程序在于接受那个能够与我们的经验相符的最简单定律为真。
6.3631 然而,这个程序没有逻辑上的证明,而只有心理学上的证明。显然,没有理由相信最简单的情况实际上会实现。
6.36311 太阳明天会升起是一个假说:这意味着我们不知道它是否会升起。
6.37 没有强迫使得一件事发生是因为另一件事已经发生了。唯一存在的必然性是逻辑必然性。
6.371 整个现代的世界观是建立在这样一个幻觉之上:即所谓的自然定律是对自然现象的解释。
6.372 因此,今天的人们停留在自然定律上,将其视为不可侵犯的东西,就像在过去时代对待上帝和命运一样。事实上,两者既对也错:尽管古代人的观点更清晰,因为他们有一个明确和公认的终点,而现代系统则试图使其看起来仿佛一切都得到了解释。
6.373 世界独立于我的意志。
6.374 即使我们所希望的一切都发生了,这仍然可以说只是命运的恩惠:因为意志和世界之间没有逻辑连接来保证这一点,而所谓的物理连接本身肯定不是我们可以意愿的东西。
6.375 正如唯一存在的必然性是逻辑必然性一样,唯一存在的不可能性也是逻辑不可能性。
6.3751 例如,两种颜色同时出现在视觉场中的同一位置是不可能的,事实上是逻辑上不可能的,因为它被颜色的逻辑结构排除了。让我们思考一下这种矛盾在物理学中是如何出现的:或多或少如下——一个粒子不能同时具有两种速度;也就是说,它不能同时在两个地方;也就是说,同时在不同地方的粒子不能是同一的。(很清楚,两个基本命题的逻辑积既不能是同义反复,也不能是矛盾。视觉场中的一个点同时具有两种不同颜色的陈述是一个矛盾)。
6.4 所有命题都具有同等的价值。
6.41 世界的意义必须位于世界之外。在世界中,一切都如其所是,一切都如其发生那样发生:其中不存在价值——如果存在,它也不会有价值。如果存在任何具有价值的价值,它必然位于所发生和是其所是的一切事物的整个领域之外。因为所有发生和是其所是的事物都是偶然的。使它非偶然的东西不能位于世界之内,因为如果它位于世界之内,它本身也会是偶然的。它必须位于世界之外。
6.42 因此,也不可能有伦理学命题。命题不能表达任何更高的东西。
6.421 显然,伦理学不能用语言表达。伦理学是先验的(transcendental)。(伦理学和美学是同一回事)。
6.422 当一个形式为“汝应……”的伦理定律被规定时,人们的第一个想法是:“如果我不做,那又会怎样?”。然而,显然伦理学与通常意义上的惩罚和奖励无关。因此,我们关于一个行为后果的问题必须是不重要的。——至少这些后果不应该是事件。因为我们提出的问题一定有其正确之处。确实必须存在某种伦理奖励和伦理惩罚,但它们必须存在于行动本身之中。(而且同样清楚的是,奖励必须是某种令人愉快的,惩罚是某种令人不愉快的)。
6.423 在意志是伦理属性的主体时,谈论它是不可能的。而作为现象的意志只对心理学感兴趣。
6.43 如果意志的善恶运用确实改变世界,它只能改变世界的界限,而不是事实——不是可以用语言表达的东西。简而言之,其效果必须是世界变成一个完全不同的世界。它必须作为一个整体来说,可以说是增长和消亡。幸福的人的世界与不幸福的人的世界是不同的。
6.431 同样地,在死亡时世界不会改变,而是终结。
6.4311 死亡不是生命中的一个事件:我们没有活到经历死亡。如果我们将永恒(eternity)理解为不是无限的时间持续,而是无时间性(timelessness),那么永恒的生命属于那些活在当下的人。我们的生命没有终结,正如同我们的视觉场没有界限一样。
6.4312 人类灵魂的时间不朽,即它在死后永远存活,不仅没有保证;而且,无论如何,这个假设完全未能实现它一直以来的目的。难道我永远存活就解决了某个谜题吗?难道这个永恒的生命本身不就像我们现在的生活一样是一个谜题吗?生命在空间和时间中的谜题的解决方案位于空间和时间之外。(肯定不需要解决任何自然科学的问题)。
6.432 世界上事物如何存在,对于那更高的东西来说是完全无关紧要的。上帝不会在世界中启示祂自己。
6.4321 事实都只对设定问题做出贡献,而不是对其解决方案做出贡献。
6.44 世界上事物如何存在并不是神秘的,而是它存在。
6.45 从永恒的视角(sub specie aeterni)看待世界,就是将其视为一个整体——一个有限的整体。感觉世界是一个有限的整体——这才是神秘的东西。
6.5 当答案不能用语言表达时,问题也不能用语言表达。谜题不存在。如果一个问题可以被提出,那么它也可能被回答。
6.51 怀疑主义不是不可驳倒的,而是显然无意义的,当它试图在不能提出问题的地方提出疑问时。因为疑问只能存在于存在问题的地方,问题只能存在于存在答案的地方,而答案只能存在于可以言说某事的地方。
6.52 我们感到,即使所有可能的科学问题都得到了回答,生命的问题仍然完全没有被触及。当然,那时就没有留下任何问题了,而这本身就是答案。
6.521 生命问题的解决方案体现在问题的消失之中。(这难道不是那些在长期怀疑之后发现生命的意义对他们来说变得清晰的人,随后却无法说出这个意义是什么的原因吗?)。
6.522 确实存在无法用语言表达的事物。它们会自我显现。它们就是神秘的东西。
6.53 哲学中正确的方法实际上应该是:只说可以言说的事物,即自然科学的命题——即与哲学无关的事物——然后,每当有人想说形而上学的东西时,就向他证明他未能赋予其命题中的某些符号意义。尽管这对另一个人来说不会令人满意——他不会觉得我们是在教他哲学——但这种方法将是唯一严格正确的方法。
6.54 我的命题就是以这种方式起着阐明(elucidatory)的作用:理解我的人,最终会认识到它们是无意义的(senseless),因为他已经通过它们、在它们之上、跨越它们爬了出去。(他必须在爬上去之后,可以说,扔掉梯子)。他必须超越这些命题,然后他就会正确地看待世界。